This following is a brief summary of our research meeting on 2024-07-05.

What happened

• Liam presented a solution to Exercise 1a in Section 1.2. By first completing the squares, he was able to rewrite the equation
  $x^2+4y^2+2x-16y+1=0$
  as the equation
  $\frac{1}{4^2}(x+1{)}^2+\frac{1}{2^2}(y-2{)}^2=1.$
  He then recognized this as an equation of an ellipse, centered at $(-1,2)$ with "horizontal radius" $4$ and "vertical radius" 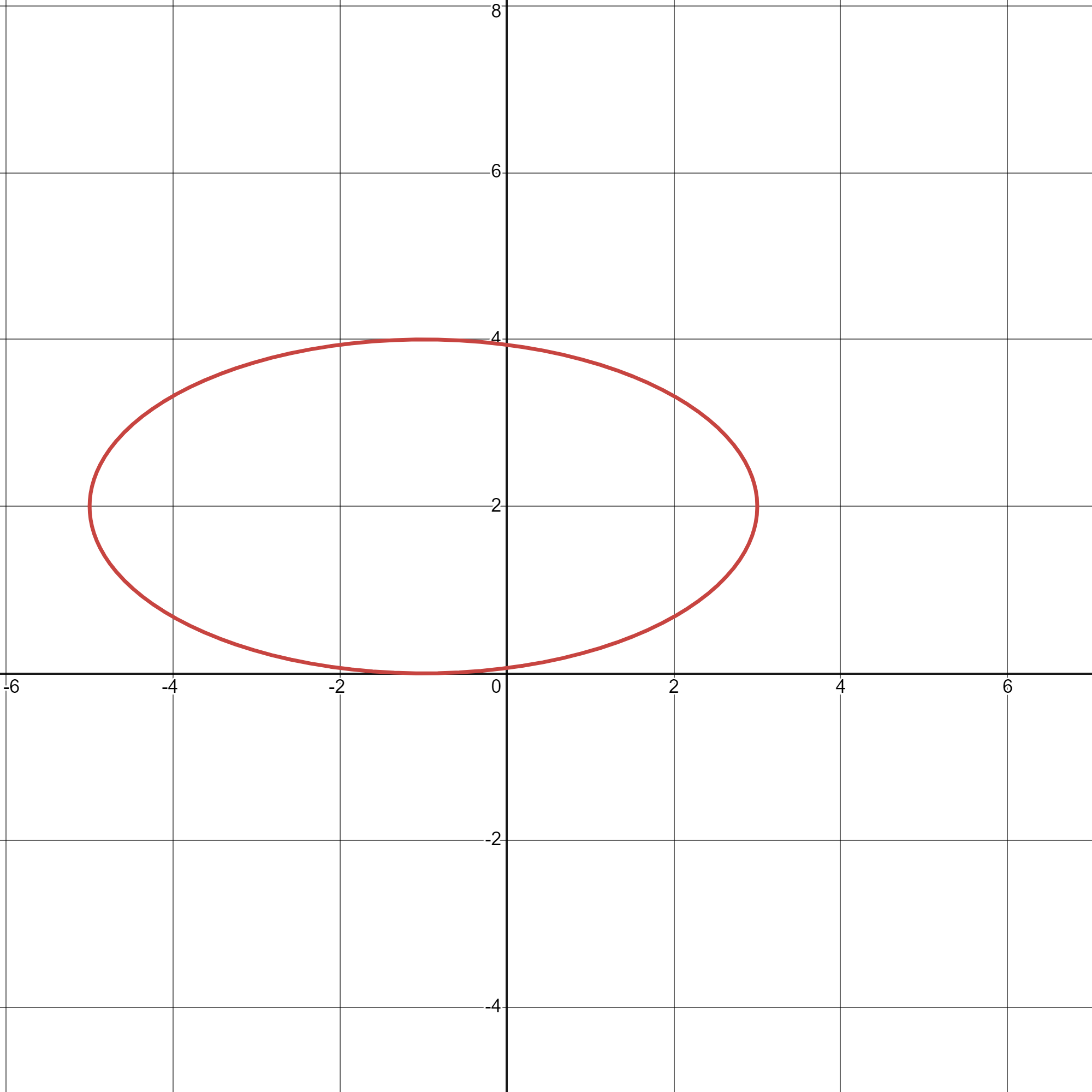$2$:

  

• Nicholas presented a solution to Exercise 1b in Section 1.2, noting that the equation $x^2-y^2=0$ was equivalent to the conditions that either $x=y$ or $x=-y$. (This can be seen either by solving the equation for $y$, or by factoring as $(x-y)(x+y)=0$.) Thus, the solution set was the union of two lines:

  

• Aaron presented a solution of Exercise 4d, noting that the equation $x{z}^2-xy=0$ is equivalent to the conditions that either $x=0$ or $y=z^2$. Thus, the solution set was the union of the plane $x=0$ and the parabolic cylinder 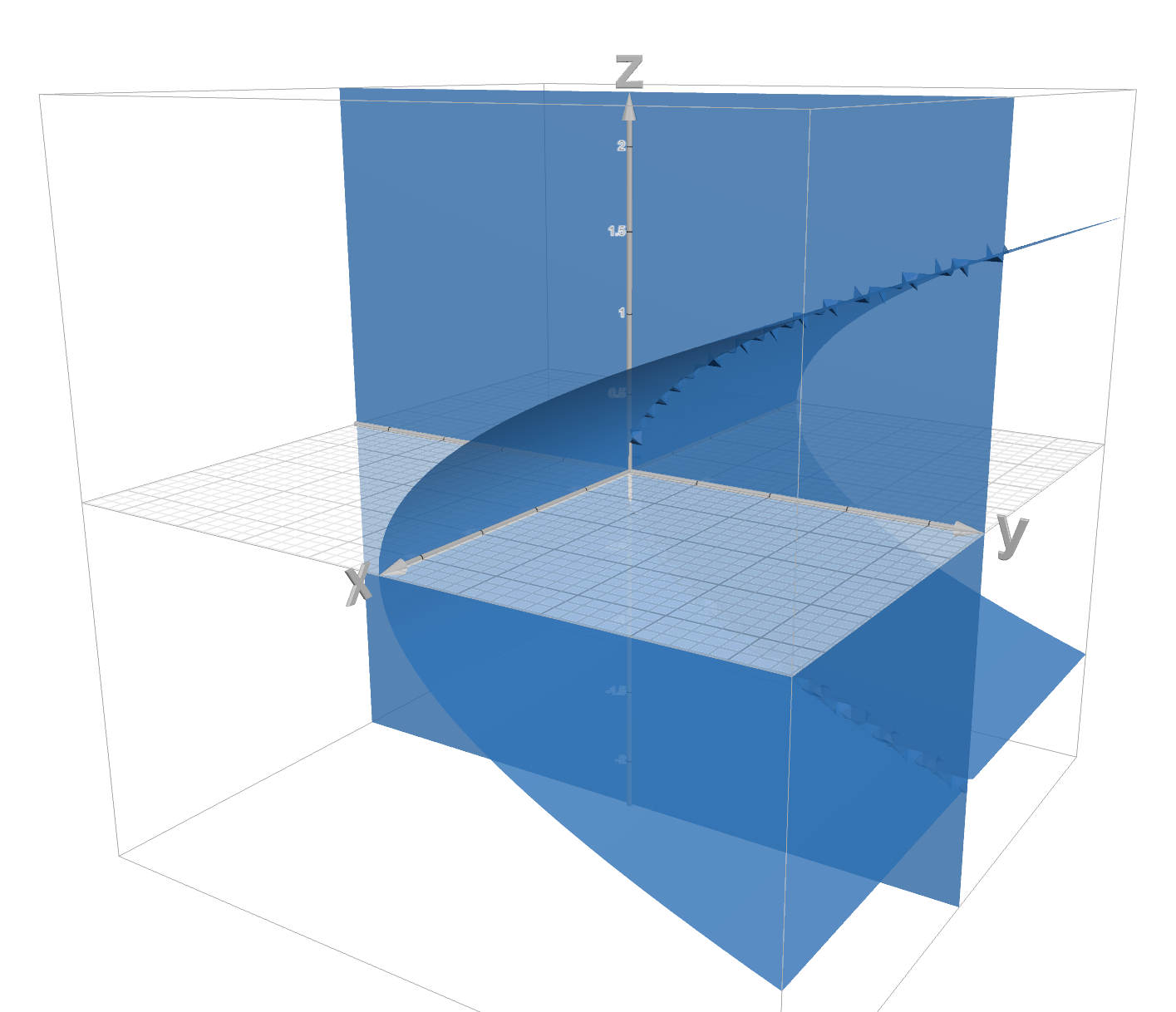$y=z^2$:

  
  (Ignore the janky edges. Those are rendering errors in the Desmos 3D visualizer.)

• Aaron also sketched the solution to Exercise 8 in Section 1.2, following the solution strategy outlined in the book. The crux of the argument relied on the fact that a polynomial in one variable has at most a finite number of zeroes.

Tasks for next meeting

• Read/skim Section 1.4, 4.1–4.3, and Sections 5.1, 5.2 and 5.4
• Work through the following exercises:
  • 1.4: 1, 3, 5, 7, 8, 15
  • 4.1: 1, 2
  • 4.2: 3, 5
  • 5.1: 2