This following is a brief summary of our research meeting on 2024-08-20.

We chatted about the problem of determining intersections of two congruence varieties, specifically the types of quadratic congruence varieties that "cover" a tropical conic with the types of linear congruence varieties that "cover" a tropical line.

When focused on a specific example. We first took a tropical conic of type $B_1$, specifically the bend locus of $f(x,y)=(0\odot x^{\odot 2})\oplus (1\odot x\odot y)\oplus (0\odot y^{\odot 2})\oplus (1\odot x)\oplus (3\odot y)\oplus 0$. We then looked specifically at the congruence variety "generated by the $y$ term", namely the congruence variety given by the tropical equation

This congruence looks like

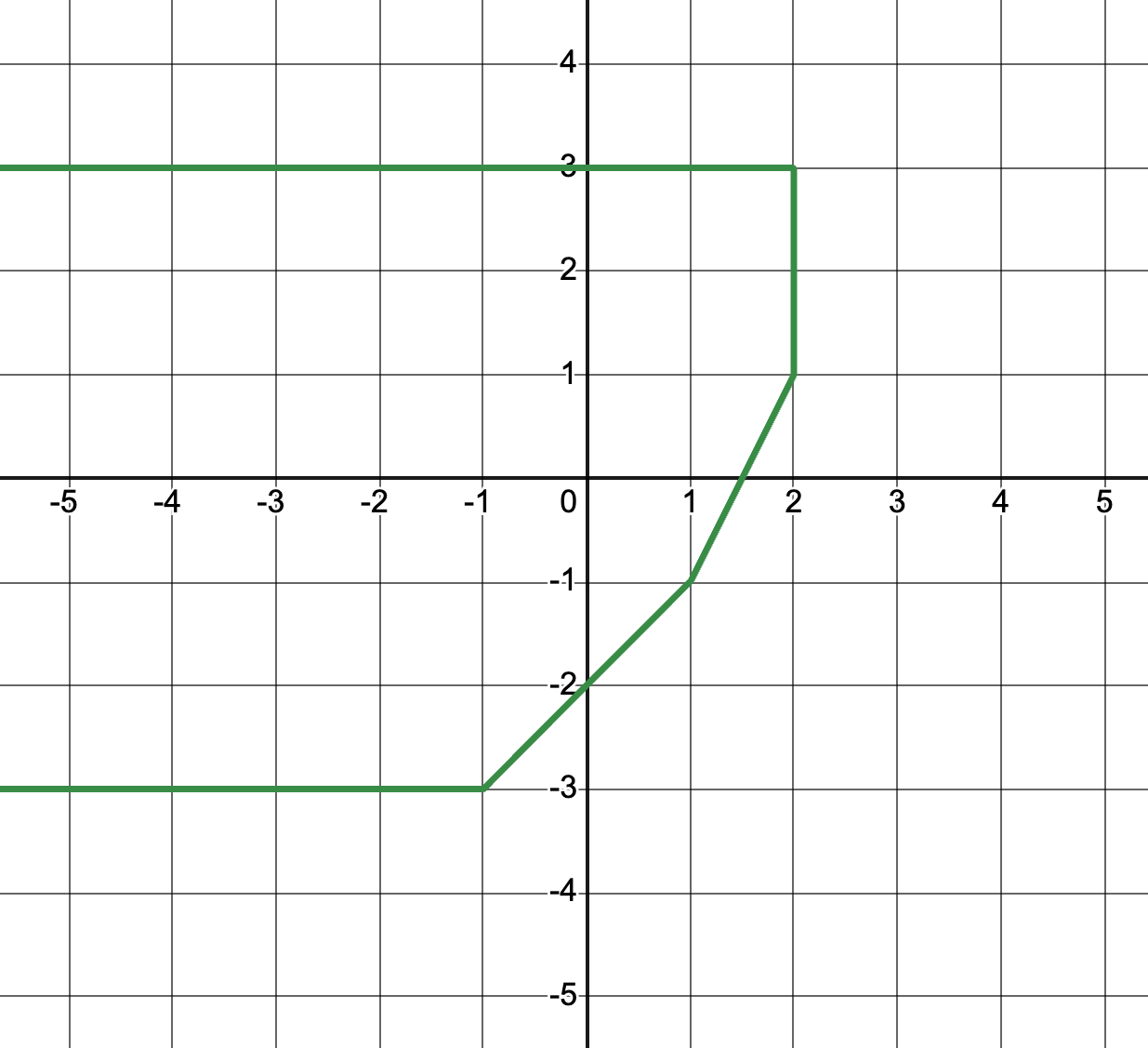
Then we looked at a tropical line that did not intersect this congruence variety, namely the bend locus of $g(x,y)=(-5\odot x)\oplus (-4\odot y)\oplus 0$. We specifically looked at the linear congruence variety "generated by the $x$ term", namely the linear congruence variety given by the tropical equation

The two congruence varieties look like

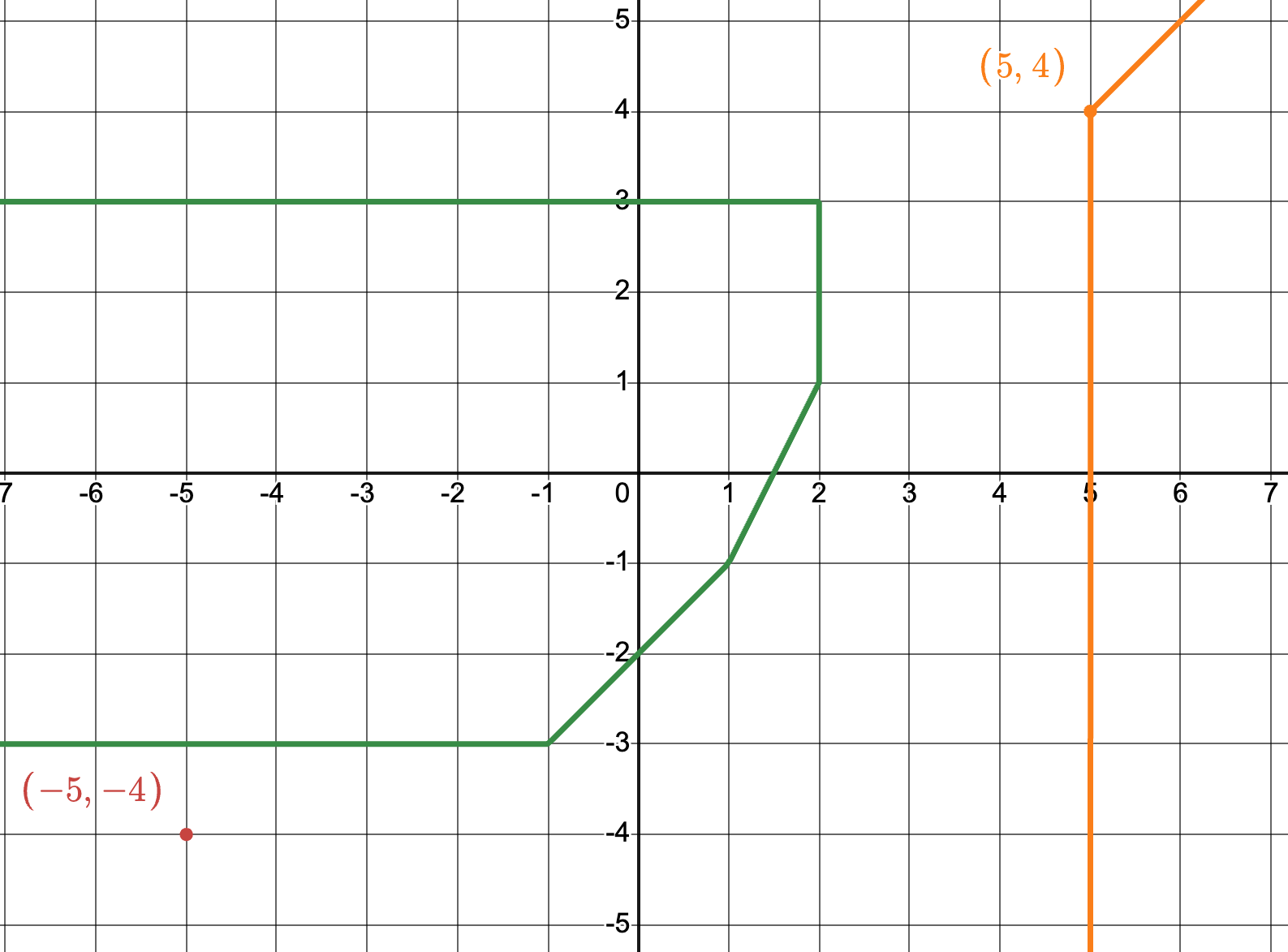
Finally, following the idea in the classical case, we solved the linear congruence for $x$ to obtain $x=(1\odot y)\oplus 5$, and then substituted that into the quadratic congruence variety (for the green curve) to get the equation

After some tropical algebra, this eventually simplified to the tropical equation

Geometrically, we know this equation has no solutions. We can also confirm this manually by converting to real operations and considering cases. However, what we would really like is a simple algebraic method to detect that this equation has no solutions, analogous to how the discriminant can detect the number of solutions to a classical quadratic equation.

Tasks for next meeting

• Try moving the linear congruence around and repeating the above analysis.
• Can you find that last quadratic equation for the general linear congruence of the form $s\odot x=(t\odot y)\oplus 0$?
• What conditions on $s$ and $t$ correlate (geometrically) with there being no solutions? two solutions? a "segment" of solutions?
• Try switching up the type of linear congruence, e.g., use the linear congruence variety "generated by the $y$ term".
• Try switching up the type of quadratic congruence, e.g., use the quadratic congruence variety "generated by the $x$ term".
• Is there a tropical analogue of the discriminant, that can detect when a tropical equation has no solutions, etc.?