Investigation into tropical tangency loci
I'm going to post ongoing work here, first in a super rough format (but eventually tidied up!)
Examples for each type of conic
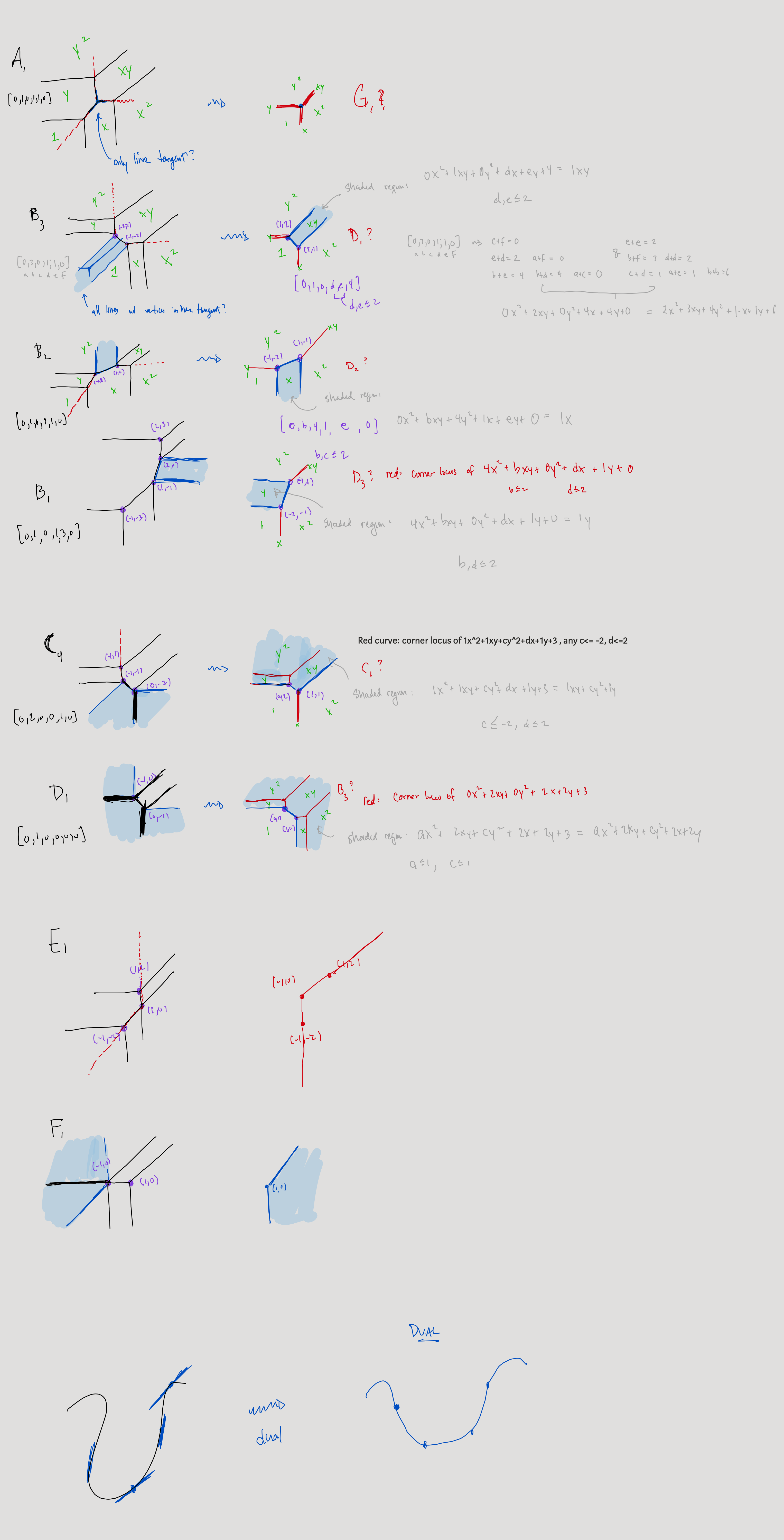
Analysis of Type
The general tropical conic of Type
(coming soon)
Almost all tropical lines intersect such conics in two distinct points:
(coming soon)
As we move the tropical line around, we can see that there is exactly one situation in which pairs of distinct intersection points converge to a single point, namely the case in which the tropical line has its vertex exactly at the "central vertex" of the conic:
(coming soon)
However, there are also some cases in which the tropical line intersects the conic along an edge, such as below. One might reasonably argue that these lines should also count as tangent. The vertex locus of such lines is the set of three rays shown below:
(coming soon)
If we take the union of the green and orange vertex loci and then rotate them 180 degrees, we have a visualization of the proposed dual locus:
(coming soon)
Conclusion
In the case of tropical conics of Type
- the dual locus is a single point; or
- the dual locus is a tropical line.
My gut instinct is that the "correct" dual locus is the second option and, moreover, that what we are seeing is really a double line. In other words, if the dual locus is actually a bend locus, then it's a tropical conic of Type; if it's a congruence variety, then it's a quadratic congruence variety that results in a double line.
Analysis of Type
Type
The general tropical conic of Type
Most tropical lines intersect such a conic in two distinct points:
As we move the tropical line around, we can see that sometimes the two distinct intersection points come together to a single point. It seems reasonable that when this happens, such tropical lines should be considered tropically tangent to the conic:
If we plot the locus of vertices of all such tropically tangent lines for this conic, we get the following shaded region:
There are some tropical lines that could either be considered tangent or secant. It's hard to say for sure. Consider the tropical line below:
If one were to move the vertex of the above line slightly to the right, suddenly we would see two intersection points that were quite far away from each other. In other words, it doesn't feel like this one intersection point is the limit of some family of pairs of intersection points that come together in a limit. That would be a case against calling such a line tropically tangent. On the other hand, I can also see a case for calling such a line tangent. The vertex locus of such lines is the pair of orange rays below:
If we take the union of the green and orange vertex loci and then rotate them 180 degrees, we have a visualization of the proposed dual locus:
Conclusion
If my intuition for the dual locus of a Type
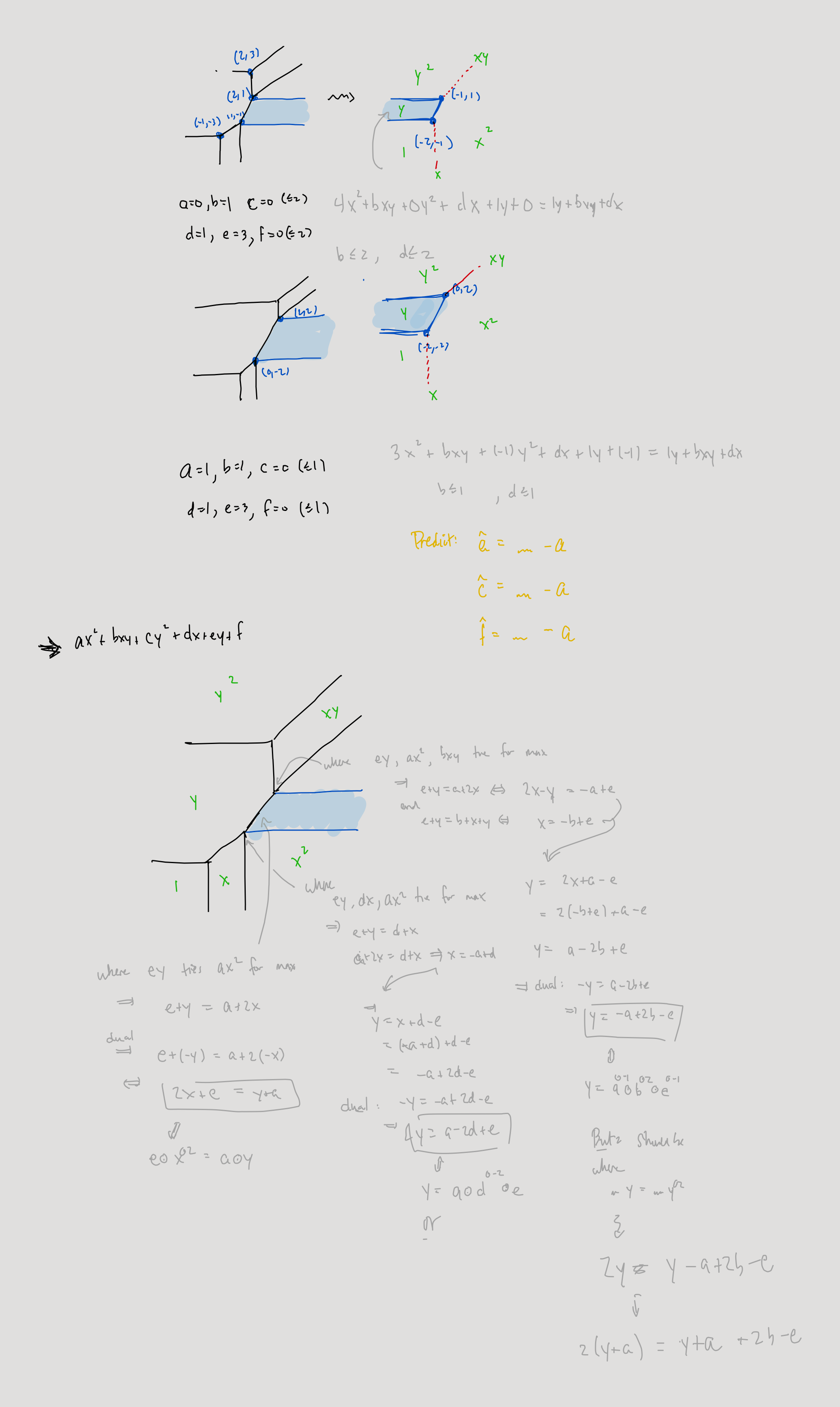
Type
Type
