Fourier transform I - Pushing Fourier series to the limit

We are about to discover the Fourier transform as the natural answer to the following:

Question

Can we extend the machinery of the Fourier series to non-periodic function?

Recap of the periodic situation

As a quick recap, we started by attempting to represent functions $f (t)$ that were periodic with period $1$ by complex Fourier series, i.e., series of the form

\sum_{n = - \infty}^{\infty} c_{n} e^{2 π i n t} .

We quickly saw that if $f (t)$ could be represented by such a series, then the coefficients in that series satisfied the integral formula

c_{n} = \int_{0}^{1} f (t) e^{- 2 π i n t} d t .

We then introduced the "hat" notation $\hat{f} (n)$ for the value of the above integral.

Eventually we used ideas from linear algebra to clarify the situation, introducing an analogue of the dot product for periodic functions, namely the inner product for functions $f, g : [0, 1] \to C$ defined by

(f, g) = \int_{0}^{1} f (t) \overset{―}{g (t)} d t .

This inner product shares nearly all of the familiar properties of the dot product on $R^{n}$ and allowed us to define both the notion of length (using $| f |^{2} = (f, f)$ ) and orthogonality (by declaring $f$ and $g$ orthogonal whenever $(f, g) = 0$ ). In particular, if we let $e_{n} (t) = e^{2 π i n t}$ , then the set of functions ${e_{n} (t) ∣ n \in Z}$ is an orthonormal set, i.e., is a set of functions that are unit length and mutually orthogonal.

With this new linear algebra language, our work above became a standard result about orthonormal sets, namely that if $f$ can be written as a linear combination of the $e_{n}$ , then that combination must be exactly

f = \sum_{n = - \infty}^{\infty} (f, e_{n}) \cdot e_{n},

where by definition

(f, e_{n}) = \int_{0}^{1} f (t) \overset{―}{e_{n} (t)} d t = \int_{0}^{1} f (t) e^{- 2 π i n t} d t = \hat{f} (n) .

The more general situation

We can easily extend the above results to the case of functions that are periodic with arbitrary period $T > 0$ . In this case, an inner product for functions $f, g : [0, T] \to C$ is given by

(f, g) = \int_{0}^{T} f (t) \overset{―}{g (t)} d t,

and our corresponding orthonormal set of "elementary" periodic functions (with period $T$ ) is ${e_{n} (t) ∣ n \in Z}$ , where $e_{n} (t) = \frac{1}{\sqrt{T}} e^{\frac{2 π i n t}{T}}$ .

Just as above, we have that for every function $f$ that's periodic function with period $T$ , if $f$ can be written as a linear combination of the orthonormal functions above, then that combination must be

f = \sum_{n = - \infty}^{\infty} (f, e_{n}) \cdot e_{n},

where

(f, e_{n}) = \int_{0}^{T} f (t) \cdot \frac{1}{\sqrt{T}} e^{- \frac{2 π i n t}{T}} d t = \frac{1}{\sqrt{T}} \int_{0}^{T} f (t) e^{- \frac{2 π i n t}{T}} d t .

If, for some reason, we wish to express $f$ as a linear combination of the functions $e^{\frac{2 π i n t}{T}}$ (which are no longer unit length but are still mutually orthogonal), we can equivalently write

f (t) = \sum_{n = - \infty}^{\infty} c_{n} e^{\frac{2 π i n t}{T}},

where $c_{n}$ satisfy the integral equation

c_{n} = \frac{1}{T} \int_{0}^{T} f (t) e^{- \frac{2 π i n t}{T}} d t .

We can now ask the question:

Can we let

T \to \infty

In other words, what happens if $f$ is not periodic? Can we make sense of some type of limit of the above situation?

Let's try answering this question in a particular (hopefully insightful) example.

Extended example: The rectangle function

Thinking like physicists for the moment, suppose we consider the simple situation of a "signal" that's "on" for one unit of time (say, $1$ second) and then "off" at all other times. We can model such a signal with a function that takes the value $1$ over an interval of length $1$ , and then value $0$ everywhere else. It will turn out to make things slightly nicer numerically if we use the function that is $1$ on the interval $[- \frac{1}{2}, \frac{1}{2}]$ and $0$ everywhere else. The graph of this function is

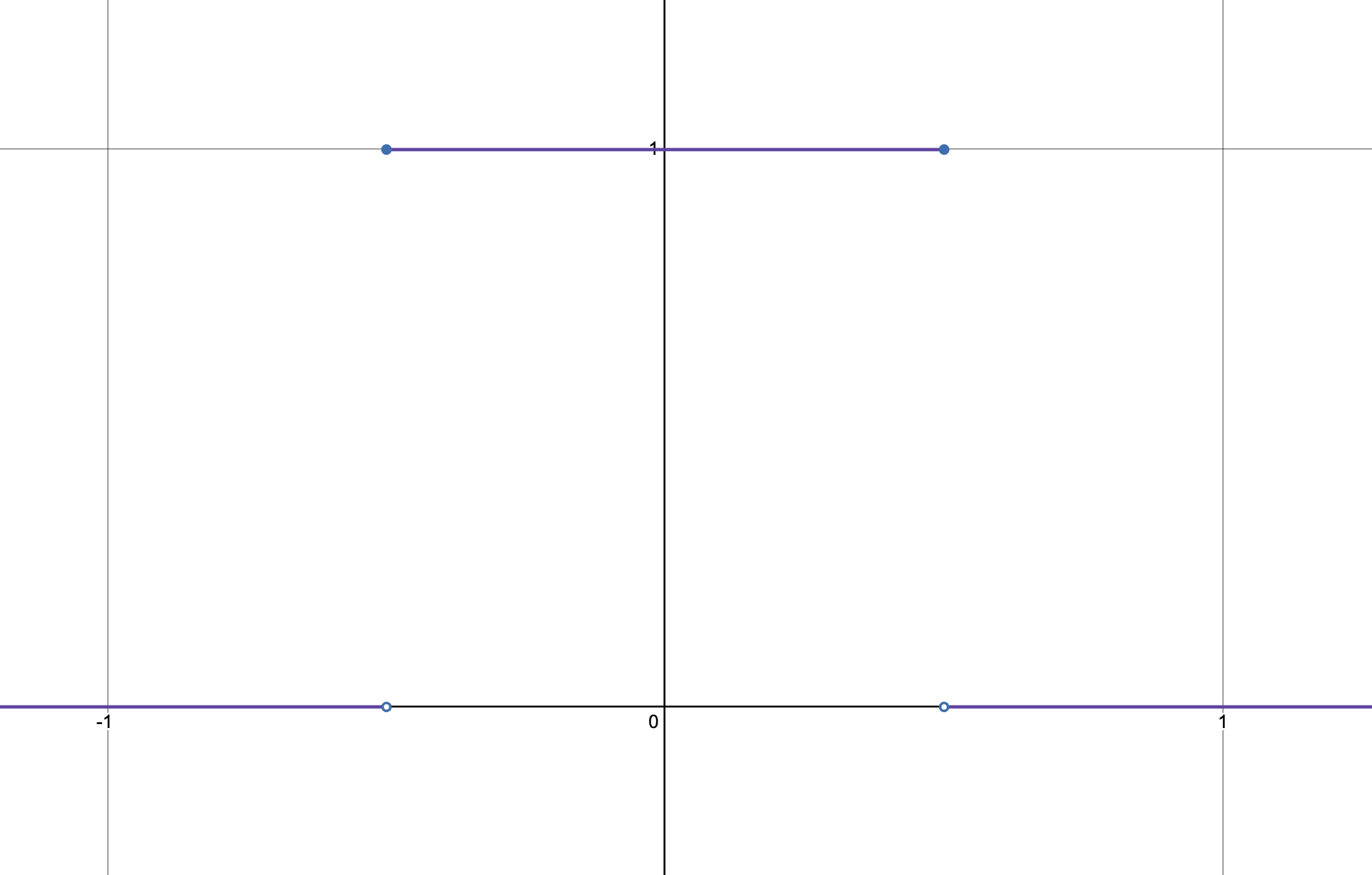
We can make this graph more visualizing appealing (and look more like an idealization of an actual, continuous signal) if we add dotted lines connecting the "jump" points:

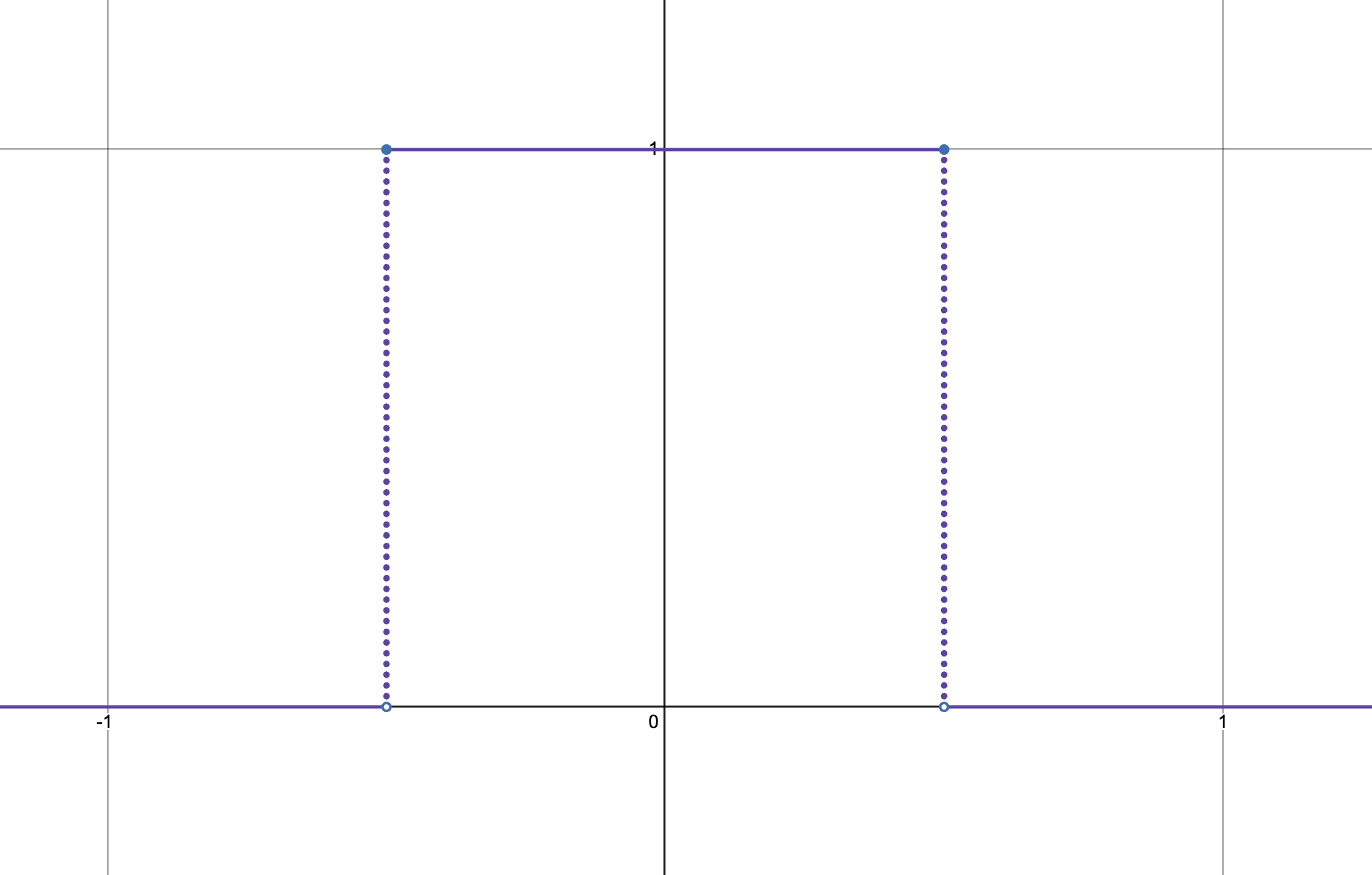
We will follow the common convention and denote this function $Π (t)$ , so that algebraically

Π (t) = {\begin{cases} 1, & if - \frac{1}{2} \leq t \leq \frac{1}{2} \\ 0, & else \end{cases}

The choice of the character $Π$ (which is a capital pi) is meant to visually remind us of the graph of the function.

It would be reasonable to call this the square function, as its graph resembles a little unit square sitting on the origin, but for historical reasons it's usually called the unit rectangle function. (This naming will seem more justified when we start stretching and scaling the function, in which case the graph resembles a non-square rectangle.)

No matter what we call it, this function is decidedly not periodic. We can easily create periodic "versions" of this function, i.e., a function that is "on" for $1$ second bursts, periodically. For example, we might want a function that agreed with the above function on $[- 1, 1]$ but that was periodic with period $2$ . In other words, suppose we considered the function $Π_{2} (t)$ whose graph looked like

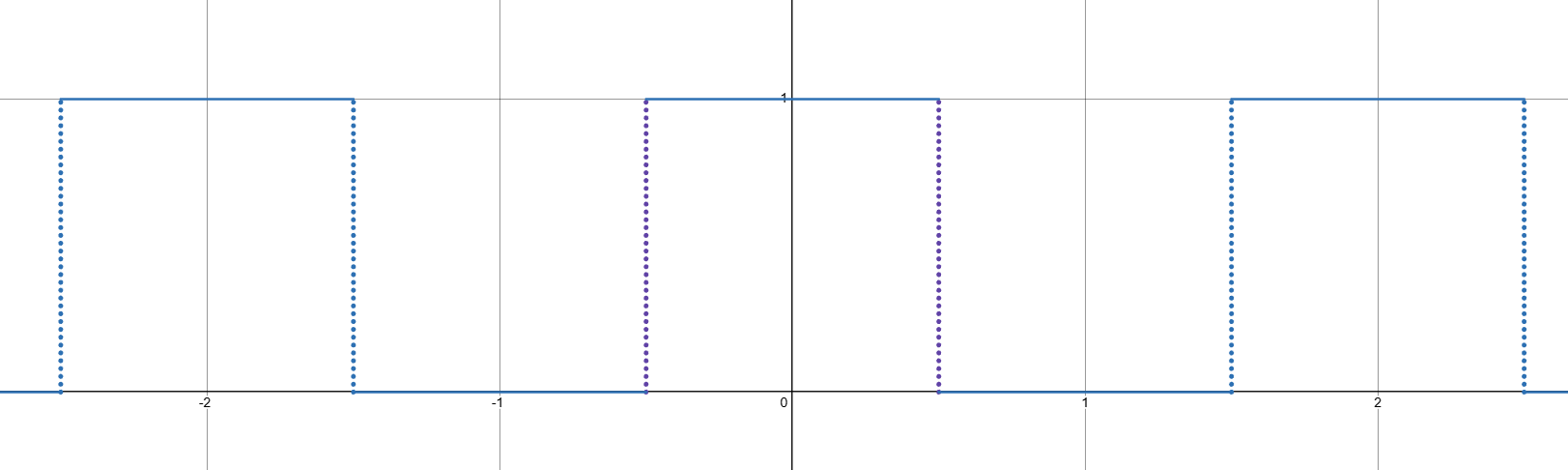
Similarly, if we wanted a function that was "on" for $1$ -second intervals every $4$ seconds, we could consider the function $Π_{4} (t)$ whose graph looked like

In general, for every $T > 1$ let's let $Π_{T} (t)$ denote the function that is periodic with period $T$ and takes the value $1$ on $[- \frac{1}{2}, \frac{1}{2}]$ . This function takes the value $1$ on every interval of the form $[k T - \frac{1}{2}, k T + \frac{1}{2}]$ , and is $0$ elsewhere.

Observations

The function $Π_{T} (t)$ is periodic with period $T > 0$ , so it makes sense to consider its corresponding complex Fourier series.
The function $Π_{T} (t)$ agrees with the function $Π (t)$ on the interval of width $T - 1$ centered at the origin. In particular, for each fixed value of $t$ we always have $lim_{T \to \infty} Π_{T} (t) = Π (t)$ . So it looks like our functions $Π_{T} (t)$ are "converging" to the original function $Π (t)$ .

Computing the Fourier series for $Π_{T} (t)$

For simplicity, let's assume $Π_{T} (t)$ agrees with its complex Fourier series and write

Π_{T} (t) = \sum_{n = - \infty}^{\infty} c_{n, T} \cdot e^{\frac{2 π i n t}{T}} .

The Fourier coefficients in this series are then given by

\begin{aligned} c_{n, T} & = \frac{1}{T} \int_{0}^{T} Π_{T} (t) e^{- \frac{2 π i n t}{T}} d t \\ = \frac{1}{T} \int_{- \frac{T}{2}}^{\frac{T}{2}} Π_{T} (t) e^{- \frac{2 π i n t}{T}} d t \\ = \frac{1}{T} \int_{- \frac{1}{2}}^{\frac{1}{2}} 1 \cdot e^{- \frac{2 π i n t}{T}} d t \\ = {\begin{cases} \frac{1}{T}, & when n = 0 \\ \frac{1}{π n} \sin (\frac{π n}{T}), & when n \neq 0 \end{cases} \end{aligned}

where we did some simplifications (behind the scenes) after computing the final integral. Substituting this information back into our Fourier series, we see that

Π_{T} (t) = \frac{1}{T} + \sum_{n \neq 0} \frac{1}{π n} \sin (\frac{π n}{T}) e^{\frac{2 π i n t}{T}} .

We want to analyze what happens in the above expression as $T \to \infty$ . To that end, we can rewrite that summation (perhaps more suggestively) as

Π_{T} (t) = \frac{1}{T} + \sum_{n \neq 0} \frac{\sin (π \cdot \frac{n}{T})}{π \cdot \frac{n}{T}} e^{2 π i t \cdot \frac{n}{T}} \cdot \frac{1}{T} .

Why rewrite the sum in this way? We claim that doing so makes the above sum look like a Riemann sum. Indeed, suppose (for some fixed value of $t$ ) we were asked to approximate the integral below with a Riemann sum:

\int_{- \infty}^{\infty} \frac{\sin (π s)}{π s} e^{2 π i t s} d s .

Ignoring questions of convergence, the conventional approach would be to subdivide the $s$ -axis into little slices of equal length, say length $Δ s = \frac{1}{T}$ :

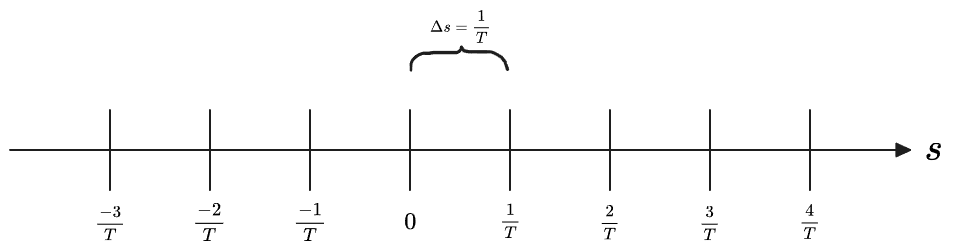
We would then evaluate the integrand at the values $s = \dots, - \frac{2}{T}, - \frac{1}{T}, 0, \frac{1}{T}, \frac{2}{T}, \dots$ , i.e., at all points of the form $s = \frac{n}{T}$ where $n \in Z$ .

A small but fixable issue

We should note that the integrand is not actually defined exactly at $s = 0$ , but we'll see shortly that as $s$ approaches $0$ the values of the integrand simply approach $1$ . In other words, the integrand has a removable discontinuity at $s = 0$ , which can be removed by setting the value of the integrand to $1$ at $s = 0$ .

With the above minor fix in mind, the Riemann sum for the above definite integral is

\int_{- \infty}^{\infty} \frac{\sin (π s)}{π s} e^{2 π i t s} d s \approx \frac{1}{T} + \sum_{n \neq 0} \frac{\sin (π \cdot \frac{n}{T})}{π \cdot \frac{n}{T}} e^{2 π i t \cdot \frac{n}{T}} \cdot \frac{1}{T},

where the first $\frac{1}{T}$ terms comes from the contribution at $s = 0$ . The sum on the right is exactly our Fourier series for $Π_{T} (t)$ !

The dramatic conclusion

Now, as we let $T \to \infty$ , our Riemann sum should converge to the exact value of the integral. In other words, we appear to have

\begin{aligned} Π (t) & = lim_{T \to \infty} Π_{T} (t) \\ = lim_{T \to \infty} (\frac{1}{T} + \sum_{n \neq 0} \frac{\sin (π \cdot \frac{n}{T})}{π \cdot \frac{n}{T}} e^{2 π i t \cdot \frac{n}{T}} \cdot \frac{1}{T}) \\ = \int_{- \infty}^{\infty} \frac{\sin (π s)}{π s} e^{2 π i t s} d s . \end{aligned}

In other words, the Fourier series for the periodic functions $Π_{T} (t)$ seem to converge to an integral representation of the non-periodic function $Π (t)$ .

An immediate question

The Fourier series for a periodic function seems to have been replaced by some type of Fourier integral for our non-periodic function. During this change, the Fourier coefficients (which were a sequence of complex numbers) were replaced by a single new function, in this case the function $\frac{\sin (π s)}{π s}$ .

How did this function arise? How is it related to our original function $Π (t)$ ?

We can answer this question by looking back at how we computed the Fourier coefficients for the periodic function $Π_{T} (t)$ . After our usual computations, we found that (at least for $n \neq 0$ )

c_{n, T} = \frac{1}{π n} \sin (\frac{π n}{T}) .

In our effort to view the Fourier series as a Riemann sum for a definite integral, we introduced the new variable $s$ , and in our sum we had $s = \frac{n}{T}$ . So, at each term in the sum we were using the approximation

\frac{\sin (π s)}{π s} \approx \frac{\sin (π \cdot \frac{n}{T})}{π \cdot \frac{n}{T}} .

Combining this estimate with the previous equality, we see that when $s = \frac{n}{T}$ we have

\begin{aligned} \frac{\sin (π s)}{π s} & \approx \frac{\sin (π \cdot \frac{n}{T})}{π \cdot \frac{n}{T}} \\ = T \cdot c_{n, T} \\ = \int_{- \frac{1}{2}}^{\frac{1}{2}} 1 \cdot e^{- \frac{2 π i n t}{T}} d t \\ = \int_{- \infty}^{\infty} Π (t) e^{- 2 π i t \cdot \frac{n}{T}} d t \end{aligned}

where in the last step we simply used the fact that $Π (t)$ was $0$ outside the interval $[- \frac{1}{2}, \frac{1}{2}]$ .

With all this in mind, it looks like (and we can now easily confirm) that

\frac{\sin (π s)}{π s} = \int_{- \infty}^{\infty} Π (t) e^{- 2 π i t s} d t

Indeed, observe that

\begin{aligned} \int_{- \infty}^{\infty} Π (t) e^{- 2 π i t s} d t & = \int_{- \frac{1}{2}}^{\frac{1}{2}} e^{- 2 π i t s} d t \\ = {[\frac{1}{- 2 π i s} e^{- 2 π i t s}]}_{t = - \frac{1}{2}}^{t = \frac{1}{2}} \\ = \frac{1}{- 2 π i s} e^{- π i s} - \frac{1}{- 2 π i s} e^{π i s} \\ = \frac{1}{2 π i s} (e^{π i s} - e^{- π i s}) \\ = \frac{1}{2 π i s} \cdot 2 i \sin (π s) \\ = \frac{\sin (π s)}{π s} . \end{aligned}

The takeaway

Here's a quick comparison between the situation for periodic functions and non-periodic functions, at least if the previous example is to be trusted.

When $f (t)$ is a periodic function with period $T > 0$ , if we can write

f (t) = \sum_{n = - \infty}^{\infty} c_{n} e^{2 π i t \cdot \frac{n}{T}},

then we must have

c_{n} = \frac{1}{T} \int_{0}^{T} f (t) e^{- 2 π i t \cdot \frac{n}{T}} d t .

On the other hand, when $f (t)$ is a non-periodic function, it seems like we might expect/hope to be able to write

f (t) = \int_{- \infty}^{\infty} F (s) e^{2 π i t s} d s,