Fourier series solutions VII - Solving differential equations with Fourier series

#differential_equations

Let's see how we can sometimes use Fourier series to help us solve differential equations, including some partial differential equations. We will give two real-world examples, both involving a concept known as heat flow. In both cases, we will be dealing with two-variable functions, where our two variables are position $x$ and time $t$ . In the first example, our function will be periodic in position, while in the second example it will be periodic in time.

Heat flow

Let's first give a quick-and-dirty derivation of the so-called "heat equation". If you're already familiar with the heat equation, you can skip to the first example.

If you're still here, then suppose something one-dimensional is heating up and $u (x, t)$ denotes the temperature at position and time (all in your favorite chosen units). Also let $q (x, t)$ denote the rate at which energy flows at position and time , where the rate is positive if the energy flows in the positive -direction.

We make two basic assumptions about the functions $u (x, t)$ and $q (x, t)$ :

Assumption 1: Newton's Law of Heating

At each fixed position $x$ , we assume the rate of energy flow with respect to time $t$ is proportional to the negative gradient (with respect to $x$ ) of temperature. In other words, if the temperature increases greatly as we move in the positive $x$ -direction, then we are assuming that the energy should flow proportionally in the direction from hot-to-cold. In terms of an equation, we are assuming

q (x, t) = - k u_{x} (x, t)

for some positive constant $k$ . Physically, the constant $k$ can be thought of as a measure of how easily energy flows across the substance when there is a temperature difference. Because of this (and unfortunate history), the reciprocal $\frac{1}{k}$ is sometimes called the thermal resistance of the substance.

Assumption 2: Energy accumulation

Suppose we look at a small chunk of the substance, of width $Δ x$ from location $x$ to location $x + Δ x$ . Let's consider the rate at which energy increases in this little piece. On the one hand, energy enters this region on the left at a rate $q (x, t)$ and exists the piece on the right at rate $q (x + Δ x, t)$ . So, the rate of change of energy in this little piece should be approximately

q (x, t) - q (x + Δ x, t) .

On the other hand, we will also assume that the rate at which energy in this little piece increases is proportional to the length of the piece and the rate at which the temperature is increasing in the piece.In other words, we will assume

q (x, t) - q (x + Δ x, t) \approx l \cdot u_{t} (x, t) \cdot Δ x

for some positive constant $l > 0$ . This constant $l$ is sometimes called the thermal capacity of the substance.

We can rewrite the above equation as

u_{t} (x, t) \approx - \frac{q (x + Δ x, t) - q (x, t)}{l \cdot Δ x} \approx - \frac{1}{l} q_{x} (x, t) .

Our second assumption is therefore that

u_{t} (x, t) = - \frac{1}{l} q_{x} (x, t) .

Combining these two assumptions

Using the above assumptions, we are suppose $u (x, t)$ and $q (x, t)$ are related by the two partial differential equations

\begin{aligned} q (x, t) & = - k u_{x} (x, t) \\ u_{t} (x, t) & = - \frac{1}{l} q_{x} (x, t) . \end{aligned}

We can combine these two differential equations to deduce a single differential equation that $u (x, t)$ must satisfy, as follows. Take partial derivatives with respect to $x$ in the first equation to obtain

q_{x} (x, t) = - k u_{x x} (x, t) .

Now substitute this into the second differential equation to obtain

u_{t} (x, t) = \frac{k}{l} u_{x x} (x, t) .

We call this equation the Heat Equation, since it gives a model for how heat behaves in a one-dimensional substance.

Example: Hot wire

Suppose we heat a thin circular wire. Let's center a polar coordinate system on this wire and let $x$ denote the position on the wire at polar angle $θ = 2 π x$ . Then let $u (x, t)$ denote the temperature of the wire at position $x$ and time $t$ .

By our choice of coordinate $x$ , the function $u (x, t)$ is periodic in $x$ with period $1$ . We now make two assumptions:

The function $u (x, t)$ satisfies the heat equation $u_{t} = u_{x x}$ .
For each fixed value of $t$ , the function $u (x, t)$ can be represented by a Fourier series in $x$ , i.e., for each value of $t$ there are complex numbers $c_{n} (t)$ such that
$u (x, t) = \sum_{n = - \infty}^{\infty} c_{n} (t) e^{2 π i n x} .$

Pay close attention to the variables

Imagine $u (x, t)$ is a family of functions of $x$ , one function at each time $t$ . Each of those functions is periodic in $x$ , so we represent it as a linear combination of our favorite periodic functions in $x$ , namely $e^{2 π i n x}$ . The coefficients of those linear combinations presumably depend on $t$ , however, which is why they're denoted $c_{n} (t)$ .

Before moving on, let's note that for each fixed value of $t$ , the coefficient $c_{n} (t)$ of $e^{2 π i n x}$ is the Fourier coefficient of the function $u (x, t)$ at index $n$ . In particular, the $n^{th}$ Fourier coefficient of $u (x, 0)$ is the coefficient $c_{n} (0)$ , and hence satisfies

c_{n} (0) = \int_{0}^{1} u (x, 0) e^{- 2 π i n x} d x .

This will come up again at the very end of this example.

Solving this partial differential equation

Let's now use the method we employed with power series (and Frobenius series), i.e., substitute our candidate series into the differential equation. In this case, let's first compute

u_{t} = \frac{\partial}{\partial t} (\sum_{n = - \infty}^{\infty} c_{n} (t) e^{2 π i n x}) = \sum_{n = - \infty}^{\infty} \frac{\partial}{\partial t} (c_{n} (t) e^{2 π i n x}) = \sum_{n = - \infty}^{\infty} c_{n}^{'} (t) e^{2 π i n x} .

(We interchanged the infinite sum and the partial differentiation, which probably deserves justification.)

On the other hand, we can also similarly compute

u_{x} = \frac{\partial}{\partial x} (\sum_{n = - \infty}^{\infty} c_{n} (t) e^{2 π i n x}) = \sum_{n = - \infty}^{\infty} \frac{\partial}{\partial x} (c_{n} (t) e^{2 π i n x}) = \sum_{n = - \infty}^{\infty} c_{n} (t) \cdot 2 π i n \cdot e^{2 π n x}

and then

\begin{aligned} u_{x x} & = \frac{\partial}{\partial x} (\sum_{n = - \infty}^{\infty} c_{n} (t) \cdot 2 π i n e^{2 π i n x}) \\ = \sum_{n = - \infty}^{\infty} \frac{\partial}{\partial x} (c_{n} (t) \cdot 2 π i n e^{2 π i n x}) \\ = \sum_{- \infty}^{\infty} c_{n} (t) \cdot 4 π^{2} i^{2} n^{2} e^{2 π i n x} \\ = \sum_{n = - \infty}^{\infty} - 4 π^{2} n^{2} c_{n} (t) e^{2 π i n x} . \end{aligned}

It follows that our Fourier series is a solution to our differential equation exactly when

\sum_{n = - \infty}^{\infty} c_{n}^{'} (t) e^{2 π i n x} = \sum_{n = - \infty}^{\infty} - 4 π^{2} n^{2} c_{n} (t) e^{2 π i n x} .

Notice that, from the point of view of the variable $x$ , both sides of this equation are linear combinations of the functions $e^{2 π i n x}$ for $n \in Z$ . Since the set of functions ${e^{2 π i n x} ∣ n \in Z}$ is a linearly independent set, the only way two linear combinations can be equal is if the coefficient of $e^{2 π i n x}$ is the same on each side, for every $n$ . In other words, we must have

c_{n}^{'} (t) = - 4 π^{2} n^{2} c_{n} (t)

for every integer $n$ .

A different kind of relation

When we looked for power series (or Frobenius series) solutions, we always found the coefficients of the mystery series needed to satisfy a recursion relation. Here, however, we see that something different has happened: the coefficients of our mystery Fourier series need to satisfy another differential equation!

You might think we've wasted our time, exchanging the problem of solving one differential equation for satisfying an entire family of new differential equations. Notice, however, that these new differential equations are ordinary, first-order, homogeneous, linear differential equations. If we fix $n$ for the moment, we can rewrite our new differential equation as

c_{n}^{'} (t) = A_{n} c_{n} (t),

where $A_{n} = - 4 π^{2} n^{2}$ is a constant. The general solution to this differential equation is

c_{n} (t) = B_{n} e^{A_{n} t},

where $B_{n}$ is any constant. In fact, if we evaluation at $t = 0$ we see that $B_{n} = c_{n} (0)$ , so we can write our solution as

c_{n} (t) = c_{n} (0) e^{- 4 π^{2} n^{2} t} .

We've done it! Under the assumptions we've made for this problem, we've proven that the general solution is

u (x, t) = \sum_{n = - \infty}^{\infty} c_{n} (0) e^{- 4 π^{2} n^{2} t} e^{2 π i n x} .

Additional observations that foreshadow some cool things

It is common to describe the solution to a differential equation using two pieces of information:

A description of the initial state of the system.
A description of how the system evolves over time, i.e., of the dynamics of the system.

In our case, the first piece of information is the function $u (x, 0)$ , which gives the initial temperature at each point $x$ on the wire. Let's denote this function $f (x)$ . This function is periodic with period $1$ and its Fourier coefficients satisfy

\begin{aligned} \hat{f} (n) & = \int_{0}^{1} f (x) e^{- 2 π i n x} d x \\ = \int_{0}^{1} u (x, 0) e^{- 2 π i n x} d x \\ = c_{n} (0) . \end{aligned}

We can now rewrite our final solution, above, as

u (x, t) = \sum_{n = - \infty}^{\infty} \hat{f} (n) e^{- 4 π^{2} n^{2} t} e^{2 π i n x} .

So now the initial state of the system can be seen as contributing to the solution. But we can do even better. Let's replace $\hat{f} (n)$ in the above sum with its integral value and then move around some terms:

\begin{aligned} u (x, t) & = \sum_{n = - \infty}^{\infty} \hat{f} (n) e^{- 4 π^{2} n^{2} t} e^{2 π i n x} \\ = \sum_{n = - \infty}^{\infty} (\int_{0}^{1} f (y) e^{- 2 π i n y} d y) e^{- 4 π^{2} n^{2} t} e^{2 π i n x} \\ = \sum_{n = - \infty}^{\infty} (\int_{0}^{1} f (y) e^{- 4 π^{2} n^{2} t} e^{2 π i n (x - y)}) \\ = \int_{0}^{1} f (y) (\sum_{n = - \infty}^{\infty} e^{- 4 π^{2} n^{2} t} e^{2 π i n (x - y)}) d y \\ = \int_{0}^{1} f (y) g (x - y, t) d y, \end{aligned}

where $g (z, t) = \sum_{n = - \infty}^{\infty} e^{- 4 π^{2} n^{2} t} e^{2 π i n z}$ .

Why did we do all of this? It turns out that our energy system (of a hot wire) is governed by:

The initial temperature information, which is function $f (x)$ that is periodic (with period $1$ ). This is sometimes called the initial impulse.
A function $g (x, t)$ that determines how the energy moves through the system. This is sometimes called the impulse response or convolving function.
The integral above, which combines the functions $f (x)$ and $g (x, t)$ , is called the convolution of the two functions. We will see that it can be seen as a "smoothed average" of the nearby temperatures, using the convolving function as a weighting function.

For now this all might seem a bit much, but as our theory develops it will prove remarkable prescient!

Example: Hot Earth

In this example, let us now imagine we've chosen a fixed position on the surface of the earth, and we let $u (x, t)$ denote the temperature $x$ meters below the surface at time $t$ (in years). This time, let us assume:

The function satisfies the heat equation $u_{t} = \frac{1}{2} u_{x x}$ . There is nothing special about the value of $\frac{1}{2}$ , other than to provide slight contrast with the previous example (and possibly make some numbers later on slightly nicer looking).
The function $u (x, t)$ is periodic in $t$ with period $1$ . In other words, at any fixed position $x$ , the temperature should repeat annually. While that's not totally realistic, it's not an entirely terrible assumption. In places like Michigan, for instance, it tends to be cold every December and hot every July. Because of this assumption, we will assume we can represent $u (x, t)$ by a Fourier series in $t$ , i.e., as
$u (x, t) = \sum_{n = - \infty}^{\infty} c_{n} (x) e^{2 π i n t} .$

Compare with the previous example

Note that in this example our function $u (x, t)$ is assumed to be periodic in time $t$ , not in position $x$ . That means our Fourier series should be a combination of our basic periodic functions in $t$ , namely $e^{2 π i n t}$ , where the coefficients depend on the position variable $x$ .

We now substitute this proposed Fourier series into our heat equation, this time finding that

\sum_{n = - \infty}^{\infty} 2 π i n \cdot c_{n} (x) e^{2 π i n t} = \sum_{n = - \infty}^{\infty} \frac{1}{2} c_{n}^{″} (x) e^{2 π i n t} .

Once again, by the linear independence of the functions ${e^{2 π i n t}}_{n}$ , the above equality implies that for all $n$ we just have

2 π i n \cdot c_{n} (x) = \frac{1}{2} c_{n}^{″} (x),

or equivalently,

c_{n}^{″} (x) = 4 π i n \cdot c_{n} (x) .

Solving this new differential equation

This new differential equation^[1] is a second-order, linear, homogeneous differential equation. We can solve it using our methods from Linear Analysis I, although there's a good chance you never worked through an example with complex coefficients like this. Fortunately, the process is the same, so long as you're familiar with how to find roots of complex numbers.

In operator notation, we can write our new differential equation as

(D^{2} - 4 π i n) c_{n} = 0,

where $D$ is the differential operator $\frac{d}{d x}$ . We now need to find the roots of the so-called auxiliary polynomial, namely $p (z) = z^{2} - 4 π i n$ . In other words, we need to find all complex numbers $z$ such that $z^{2} = 4 π i n$ . Fortunately, there is a straightforward process to do this, using exponential notation.

Suppose $z$ is one of the roots, so that $z^{2} = 4 π i n$ . Let's rewrite both sides in polar-exponential form. On the left-hand side we'll simply write $z = r e^{i θ}$ . On the right-hand side we have two cases to consider. When $n \geq 0$ , the number $4 π i n$ is purely imaginary with nonnegative imaginary part, i.e., lies on the positive imaginary axis. Its polar angle is therefore $\frac{π}{2}$ and its polar length is $4 π n$ , so in polar-exponential form this number is $4 π n \cdot e^{i \cdot \frac{π}{2}}$ . The equality $z^{2} = 4 π i n$ then becomes

r^{2} e^{i \cdot 2 θ} = 4 π n \cdot e^{i \cdot \frac{π}{2}} .

In polar-exponential form, two complex number are the same exactly when they have the same polar distance and the same angle, up to integer multiples of $2 π$ . So, the above equation implies that $r^{2} = 4 π n$ and $2 θ = \frac{π}{2} + 2 π k$ for $k \in Z$ . It follows that $r = 2 \sqrt{π n}$ and $θ = \frac{π}{4} + π k$ for $k \in Z$ . This leads to the two distinct complex numbers $z_{1} = 2 \sqrt{π n} \cdot e^{i \cdot \frac{π}{4}}$ and $z_{2} = 2 \sqrt{π n} \cdot e^{i \cdot \frac{5 π}{4}}$ .

We now repeat the previous computation in the case $n < 0$ . In that case, the number $4 π i n$ is purely imaginary with negative imaginary part, i.e., lies on the negative imaginary axis. Its polar angle is therefore $- \frac{π}{2}$ and its polar length is $4 π | n |$ , so in polar-exponential form this number is $4 π | n | e^{- i \cdot \frac{π}{2}}$ . The equality $z^{2} = 4 π i n$ then becomes

r^{2} e^{i \cdot 2 θ} = 4 π | n | e^{- i \cdot \frac{π}{2}} .

It follows that $r = 2 \sqrt{π | n |}$ and $θ = - \frac{π}{4} + π k$ for $k \in Z$ . This leads to the two distinct complex numbers $z_{3} = 2 \sqrt{π | n |} \cdot e^{- i \cdot \frac{π}{4}}$ and $z_{4} = 2 \sqrt{π | n |} \cdot e^{- i \cdot \frac{5 π}{4}}$ . (We've written the angles in this way so that it's clear $z_{1}$ and $z_{3}$ are complex conjugates, as are $z_{2}$ and $z_{4}$ ).

Before returning to our Fourier series, in this case it helps to rewrite the above complex numbers in their real and imaginary parts. Using Euler's identity, we have

z_{1} = 2 \sqrt{π n} \cdot e^{i \cdot \frac{π}{4}} = 2 \sqrt{π n} \cdot (\cos (π / 4) + i \sin (π / 4)) = 2 \sqrt{π n} \cdot (\frac{\sqrt{2}}{2} + i \cdot \frac{\sqrt{2}}{2}) = \sqrt{2 π n} (1 + i)

Similarly, we find that

\begin{aligned} z_{2} & = - \sqrt{2 π n} (1 + i) \\ z_{3} & = \sqrt{2 π | n |} (1 - i) \\ z_{4} & = - \sqrt{2 π | n |} (1 - i) . \end{aligned}

Now that we finally have these roots, we can conclude that the general solution to the second-order differential equation

(D^{2} - 4 π i n) c_{n} = 0

c_{n} (x) = {\begin{cases} A_{n} e^{\sqrt{2 π n} (1 + i) x} + B_{n} e^{- \sqrt{2 π n} (1 + i) x} & when n \geq 0 \\ A_{n} e^{\sqrt{2 π | n |} (1 - i) x} + B_{n} e^{- \sqrt{2 π | n |} (1 - i) x} & when n < 0 \end{cases}

Time to cheat

It turns out that, in our particular problem, our Fourier coefficients must have $A_{n} = 0$ for all $n$ . We will take that as a fact for now, but I encourage you to investigate what happens to our final solution (below) if we do not make that assumption.

Using the above cheat, we can now conclude that

c_{n} (x) = {\begin{cases} B_{n} e^{- \sqrt{2 π n} (1 + i) x} & when n \geq 0 \\ B_{n} e^{- \sqrt{2 π | n |} (1 - i) x} & when n < 0 \end{cases}

As usual, if we set $x = 0$ in the above expression then we obtain $c_{n} (0) = B_{n}$ , so we can rewrite the above as

c_{n} (x) = {\begin{cases} c_{n} (0) e^{- \sqrt{2 π n} (1 + i) x} & when n \geq 0 \\ c_{n} (0) e^{- \sqrt{2 π | n |} (1 - i) x} & when n < 0 \end{cases}

Even better, if we let $f (t) = u (0, t)$ (the temperature at the surface, which we can think of as the initial data for this system), then just as in the previous example we can verify that $\hat{f} (n) = c_{n} (0)$ , and so we can rewrite the previous expression as

c_{n} (x) = {\begin{cases} \hat{f} (n) e^{- \sqrt{2 π n} (1 + i) x} & when n \geq 0 \\ \hat{f} (n) e^{- \sqrt{2 π | n |} (1 - i) x} & when n < 0 \end{cases}

The solution to our "Hot Earth" problem is therefore

u (x, t) = \sum_{n = - \infty}^{- 1} \hat{f} (n) e^{- \sqrt{2 π | n |} (1 - i) x} e^{2 π i n t} + \sum_{n = 0}^{\infty} \hat{f} (n) e^{- \sqrt{2 π n} (1 + i) x} e^{2 π i n t}

Analyzing a special case

The above formula looks pretty complicated, so let's consider a special case in which a bunch of the terms greatly simplify. Suppose the temperature at the surface were given by $f (t) = \sin (2 π t)$ . Converting this function directly into complex exponential functions, we find that

f (t) = \frac{i}{2} e^{- 2 π i t} - \frac{i}{2} e^{2 π i t} .

It follows that $\hat{f} (- 1) = \frac{i}{2}$ , $\hat{f} (1) = - \frac{i}{2}$ and $\hat{f} (n) = 0$ for all other $n$ . Our giant summation above then reduces to simply

u (x, t) = \frac{i}{2} e^{- \sqrt{2 π} (1 - i) x} e^{- 2 π i t} - \frac{i}{2} e^{- \sqrt{2 π} (1 + i) x} e^{2 π i t}

We can simplify this expression and convert it into a function involving only real numbers, as follows:

\begin{aligned} u (x, t) & = \frac{i}{2} e^{- \sqrt{2 π} (1 - i) x} e^{- 2 π i t} - \frac{i}{2} e^{- \sqrt{2 π} (1 + i) x} e^{2 π i t} \\ = \frac{i}{2} e^{- \sqrt{2 π} \cdot x} (e^{i (\sqrt{2 π} \cdot x - 2 π t)} - e^{- i (\sqrt{2 π} \cdot x - 2 π t)}) \\ = \frac{i}{2} e^{- \sqrt{2 π} \cdot x} (2 i \sin (\sqrt{2 π} \cdot x - 2 π t)) \\ = - e^{- \sqrt{2 π} \cdot x} \sin (\sqrt{2 π} \cdot x - 2 π t) \\ = e^{- \sqrt{2 π} \cdot x} \sin (2 π t - \sqrt{2 π} \cdot x) . \end{aligned}

A physicist might call this a damped and phase-shifted sine function. The term $e^{- \sqrt{2 π} \cdot x}$ is the damping term, while the $- \sqrt{2 π} \cdot x$ inside the sine function causes the phase shift.

To make things even nice, suppose we fixed our attention at position $x = \sqrt{π / 2} \approx 1.25$ meters, i.e., about $4$ feet below the ground. In this case, the above expression simplifies even further to

u (\sqrt{π / 2}, t) = e^{- π} \sin (2 π t - π) .

Comparing the graph of this function with the graph of the surface temperature, we see the following:

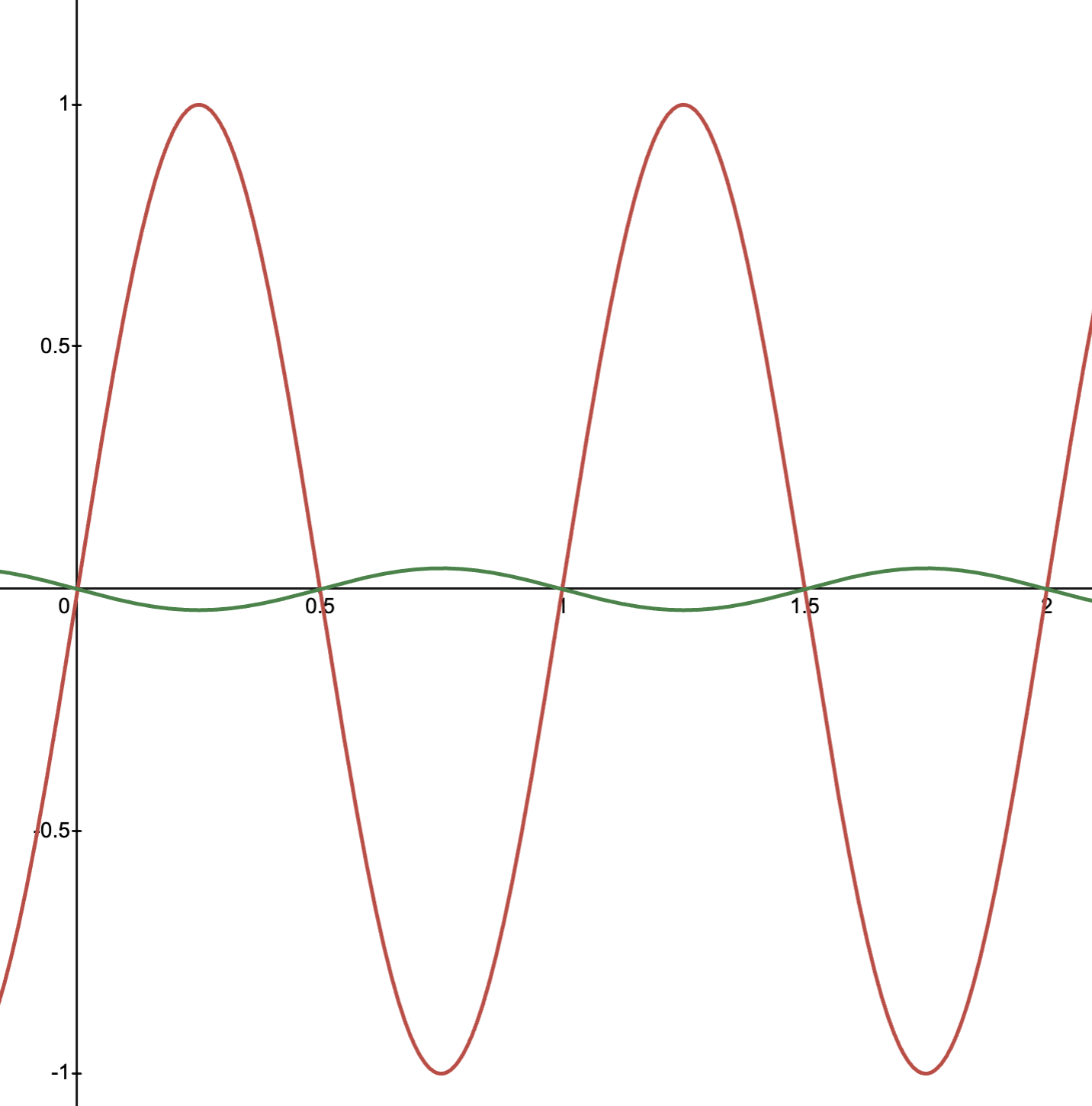
In other words, the temperature four feet down:

Doesn't vary much.
Is cool when the surface is warm and warm when the surface is cool.

This sounds a lot like how a cellar works, and it's the reason cellars are so useful!

A last observation

Before leaving this example, let's end by noting that the same trick used in the previous example can let us rewrite the general solution $u (x, t)$ in the form

u (x, t) = \int_{0}^{1} f (s) g (x, t - s) d s,

where $f (t)$ is our surface temperature (the initial impulse in our system) and where

g (x, y) = \sum_{n = - \infty}^{- 1} e^{- \sqrt{2 π | n |} (1 - i) x} e^{2 π i n y} + \sum_{n = 0}^{\infty} e^{- \sqrt{2 π n} (1 + i) x} e^{2 π i n y}

is the impulse response (aka Green's function, fundamental solution, convolving function, ...).

There's definitely something going on here, and we'll see exactly what that is when we get familiar with the Fourier transform.

Suggested next notes

Fourier transform I - Pushing Fourier series to the limit

Really a family of differential equations, one for each integer $n$ . ↩︎