Fourier series solutions I - A problem with power series

Jean-Baptiste Joseph Fourier

There cannot be a language more universal and more simple, more free from errors and obscurities...more worthy to express the invariable relations of all natural things than mathematics.

Up to this point we have been focusing on finding power series (and Frobenius series) solutions to differential equations, the ideal outcome being a complete description of the general solution. For example, in studying the differential equation $y^{″} + y = 0$ , the optimal outcome is to deduce that the general solution to the differential equation is given by

y (x) = a_{0} \sum_{\begin{matrix} n = 0 \\ n even \end{matrix}}^{\infty} \frac{(- 1)^{n / 2}}{n!} x^{n} + a_{1} \sum_{\begin{matrix} n = 0 \\ n odd \end{matrix}}^{\infty} \frac{(- 1)^{(n - 1) / 2}}{n!} x^{n} .

In fact, the ideal conclusion is to recognize the power series we discovered as representing well-known functions, such as sine and cosine in the above example:

y (x) = a_{0} \cos (x) + a_{1} \sin (x) .

We have often fallen short of this goal, however. The coefficients in our trial solutions were always found to satisfy recursion relations, and without a general machine for solving recursion relations we resorted to computing the first several coefficients in the solution. As such, we were usually forced to conclude with an "open" description of the solution, such as

y_{1} (x) = 1 - \frac{1}{6} x^{3} + \frac{1}{120} x^{5} - \dots,

with the understanding that we could compute additional terms if needed. Consequently, if we ever wanted to use our solution---to model a dynamical system, for instance---we would be forced to use an approximation, such as

y_{1} (x) \approx 1 - \frac{1}{6} x^{3} + \frac{1}{120} x^{5} .

This is akin to using a Taylor polynomial to approximate a function, rather than its full Taylor series.^[1]

The error in using that approximation generally depends on how far away from the center we evaluate the function. One unfortunate weakness of Taylor approximations is that they can rapidly transition from excellent approximations to terrible approximations. It all depends on the function being approximated.

Consider the example above, which is the Maclaurin series for the sine function. It is a theorem of calculus that this Maclaurin series perfectly matches the sine function for all real inputs. Moreover, whenever we approximate sine using the first few terms of its Maclaurin series, the resulting polynomial is the best possible approximation by a polynomial of that degree to the sine function near $x = 0$ . However, despite being the "best possible"^[2] approximation near $x = 0$ , these approximations rapidly transition from excellent to terrible as we stray away from $x = 0$ . This is readily apparent in the graphs below, which show the graph of sine together with its Taylor polynomial approximations of degrees one, three, and five.

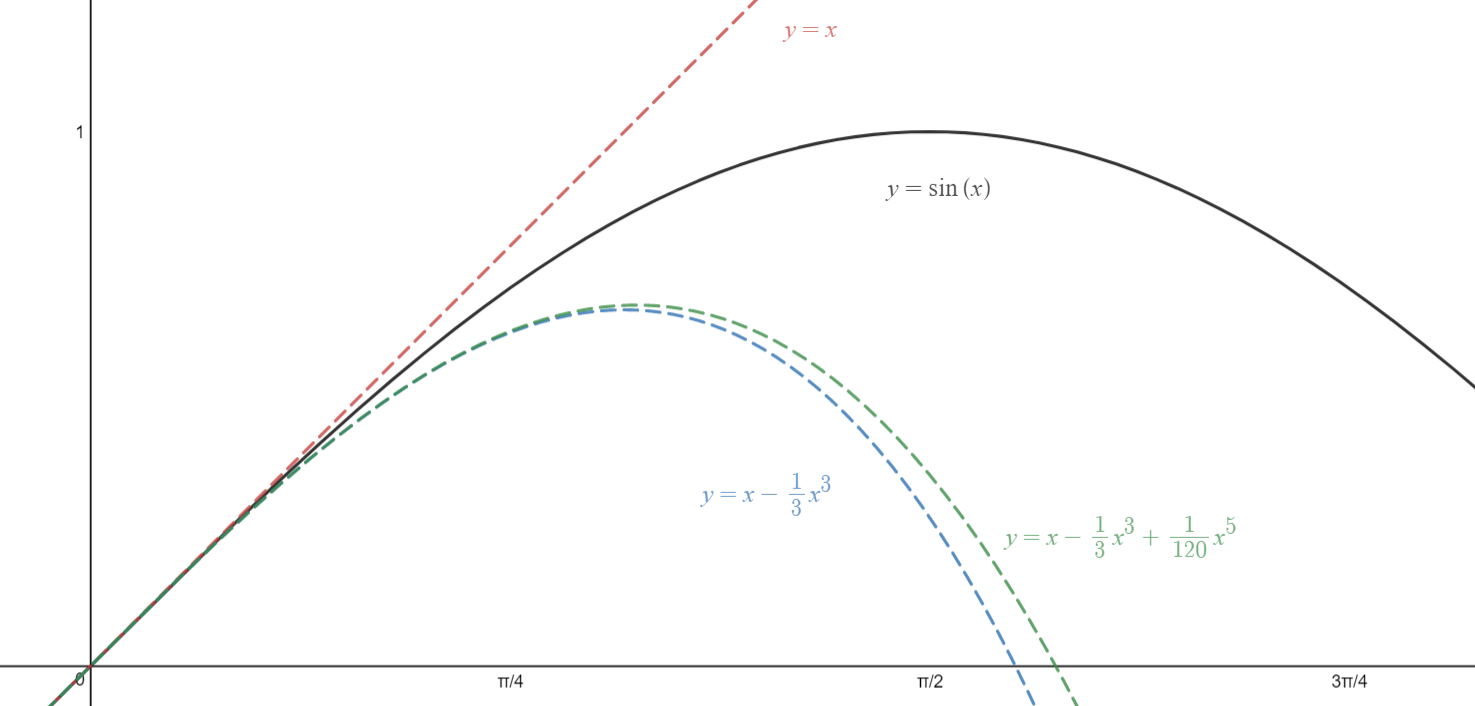
If we zoom out, we can better see the scope of the problem:

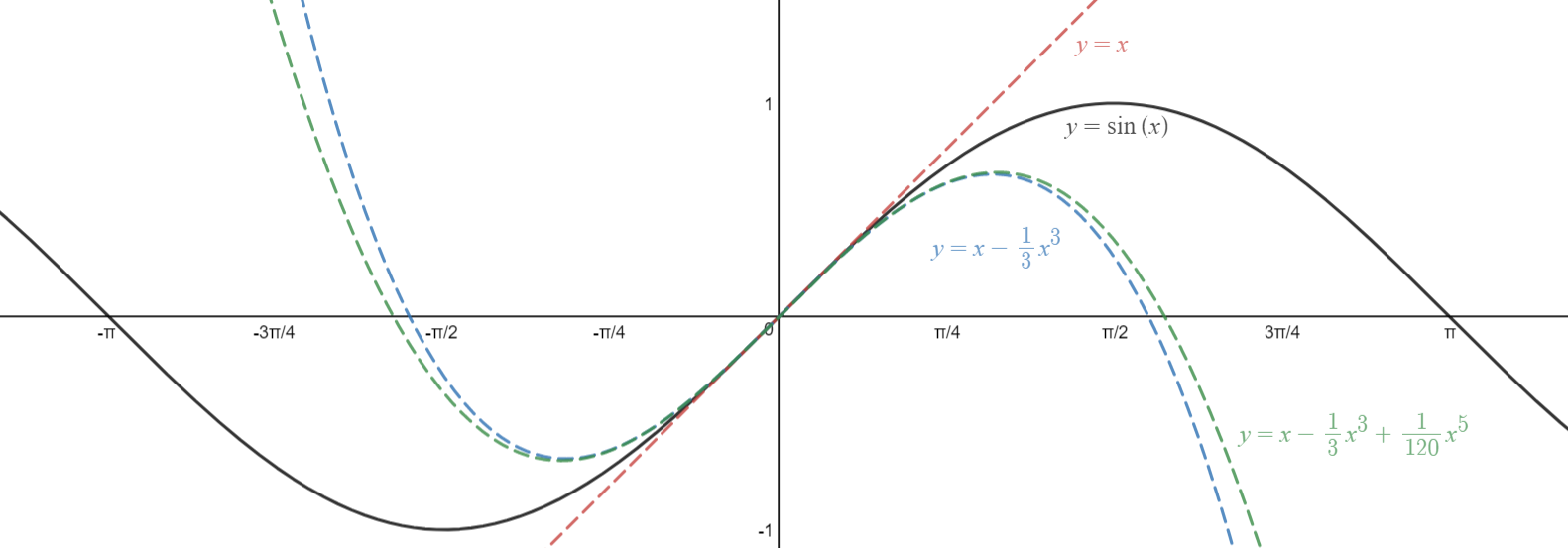
The main issue is that the behavior of sine for large $x$ is very different from that of any polynomial. Sine is a periodic function, with values forever oscillating between -1 and 1. By contrast, every nonconstant polynomial is unbounded as $x$ grows large. So no polynomial of positive degree is a good approximation to the sine function for large $x$ . This issue is not particular to the sine function. Any bounded function will have this issue, including every continuous periodic function. Is there a different type of series that is better suited to represent periodic functions?

To put things in the context of linear algebra, we can reframe the question as follows. To represent a function by a power series centered at $x_{0} = 0$ is to write that function as a linear combination of the functions $1, x, x^{2}, \dots$ , i.e., to find numbers $a_{n}$ so that

f (x) = \sum_{n = 0}^{\infty} a_{n} x^{n} .

By definition this is possible exactly when the function $f$ is analytic at $x_{0} = 0$ , and it works especially well for functions that can be "well-approximated"^[3] by polynomials. Similarly, to represent a function by a Frobenius series centered at $x_{0} = 0$ is to write that function as a linear combination of functions of the form $x^{r}, x^{r + 1}, x^{r + 2}, \dots$ , i.e., to find numbers $a_{n}$ so that

f (x) = \sum_{n = 0}^{\infty} a_{n} x^{n + r} .

This is possible when the function $f$ is at least "somewhat" analytic at $x = 0$ .

Periodic functions like sine do not seem well-suited to being approximated by linear combinations of powers of $x$ . For these types of functions, it makes sense to try to approximate with a more appropriate family of functions. That will be our next goal, one which will ultimately lead us to Fourier series. First, though, we'll briefly review properties of periodic functions.

Suggested next notes

Fourier series solutions II - Periodic functions

In this ongoing example, this is precisely the same as a Taylor polynomial approximation. ↩︎
What does "best possible" mean? That is an important question, and one that we will return to later. ↩︎
Again, we have not made clear what it means for one function to be "well-approximated" by another function. ↩︎