Some background

Origin of the term "spectral sequence"

The basic goal

A common scenario behind many (but not all!) applications of spectral sequences is to compute $H^{\bullet }$, where $H^{\ast }$ is some type of graded object (e.g., graded $R$-module, $k$-vector space, $k$-algebra, etc.). Common scenarios are:

• (co)homology of some space
• (graded) algebraic invariant of some group/ring/module
• (hyper)cohomology of a double complex

For simplicity, let's assume $H^{\bullet }$ is a "locally finite" graded vector space with finite grading, say $H^{\bullet }=\underset{r=0}{\overset{n}{⨁}}{H}^r$ with each $H^r$ a finite-dimensional $k$-vector space.

Suppose now $H^{\bullet }$ has a filtration:

For example, the grading itself can give a filtration, where

In any case, from a filtration $F^{\bullet }$ of $H^{\bullet }$ we can always construct an associated graded object (here, a graded $k$-vector space) by direct summing the successive quotients. In other words, define a graded object $G{r}^{\bullet }(F^{\bullet })$ by

Now, it's sometimes the case that we can recover $H^{\bullet }$ in this way, i.e., that $H^{\bullet }\simeq \underset{p=0}{\overset{m}{⨁}}G{r}^p(F^{\bullet })$. This is not always the case, however, and a spectral sequence can be viewed as the "best" way to address this.

Before moving onto the definition of a spectral sequence, note a filtration $F^{\bullet }$ on the graded object $H^{\bullet }$ actually results in an associated bigraded object, where

Although it might seem odd that we've chosen to write the bigrading this one, it's for historical reasons. The degree $p$ is called the filtration degree, while the degree $q$ is called the complementary degree.

We sometimes call $E_r^{\bullet ,\bullet }$ the $r^{\text{th}}$-page of the spectral sequence. Also, the above type of spectral sequence is sometimes called a spectral sequence with upward orientation, since the arrows in $E_0^{\bullet ,\bullet }$ point upward. There is an analogous definition of a spectral sequence with rightward orientation, which we'll see in examples below.

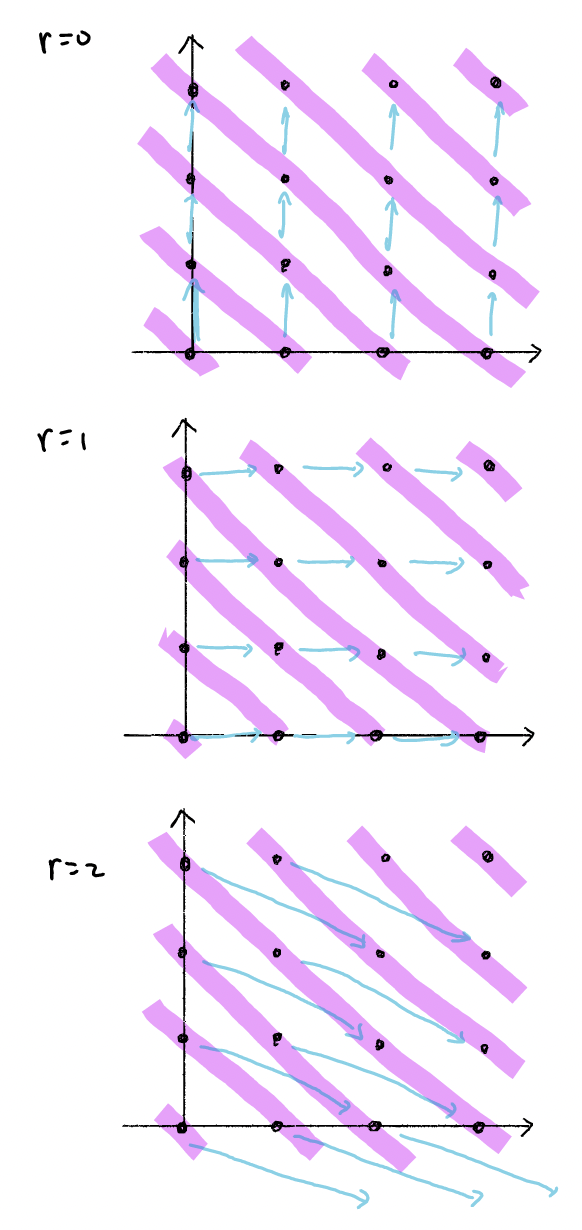
Notice that for any fixed coordinate $(p,q)$, for $r$ large enough the differentials into and out of $E_r^{p,q}$ become trivial. (In fact, we just need $r>max\{p,q+1\}$). Once this happens, we say the spectral sequence has stabilized in that coordinate and denote that final object (vector space) by $E_{\mathrm{\infty }}^{p,q}$.

The basic idea for a double complex

Suppose we start with a double complex $C^{\bullet ,\bullet }$ that has "horizontal" and "vertical" differentials:

Let's assume for simplicity that the sequares anti-commute, i.e., that $d_{\text{ver}}{d}_{\text{hor}}+d_{\text{hor}}{d}_{\text{vert}}=0$. (If they commute, we can always replace $d_{\text{vert}}^{p,q}$ with $(-1{)}^p{d}_{\text{vert}}^{p,q}$, say). The total complex associated to this double complex is the complex $C^{\bullet }$, where

and where we use the differential $d=d_{\text{vert}}+d_{\text{hor}}$. (Check that we do indeed have $d\circ d=0$.)

Now consider the cohomology $H^{\bullet }$ of this total complex $C^{\bullet }$. (This is sometimes called the total cohomology or hypercohomology of the double complex.)

There are two obvious filtrations we can put on $C^{\bullet }$, and these lead to two different spectral sequences which both converge to $H^{\bullet }$. Both spectral sequences begin with $E_0^{p,q}=C^{p,q}$. However, one spectral sequences uses $d_{\text{hor}}$ for its $d_0$ differentials; the other uses $d_{\text{vert}}$ for its $d_0$ differentials.

Example: The Snake Lemma

Suppose we begin with the commutative diagram below, in which the rows are exact:

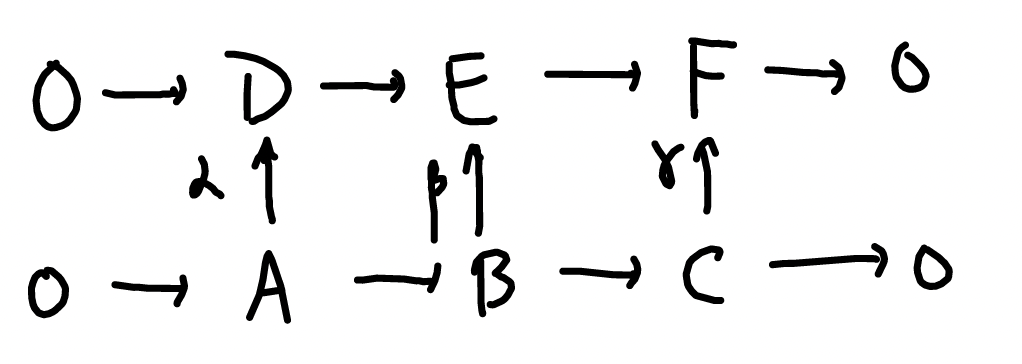
Extend this to first-quadrant double complex by putting 0s in every other position and trivial maps where needed.

Using the horizontal arrows produces a spectral sequence with rightward orientation. The pages $E_0^{\bullet ,\bullet }$ and $E_1^{\bullet ,\bullet }$ are show below. (The assumption on exactness in the rows of the original diagram implies that the cohomology at every position in this diagram vanishes. So, the page $E_1^{\bullet ,\bullet }$ would be completely trivial.)

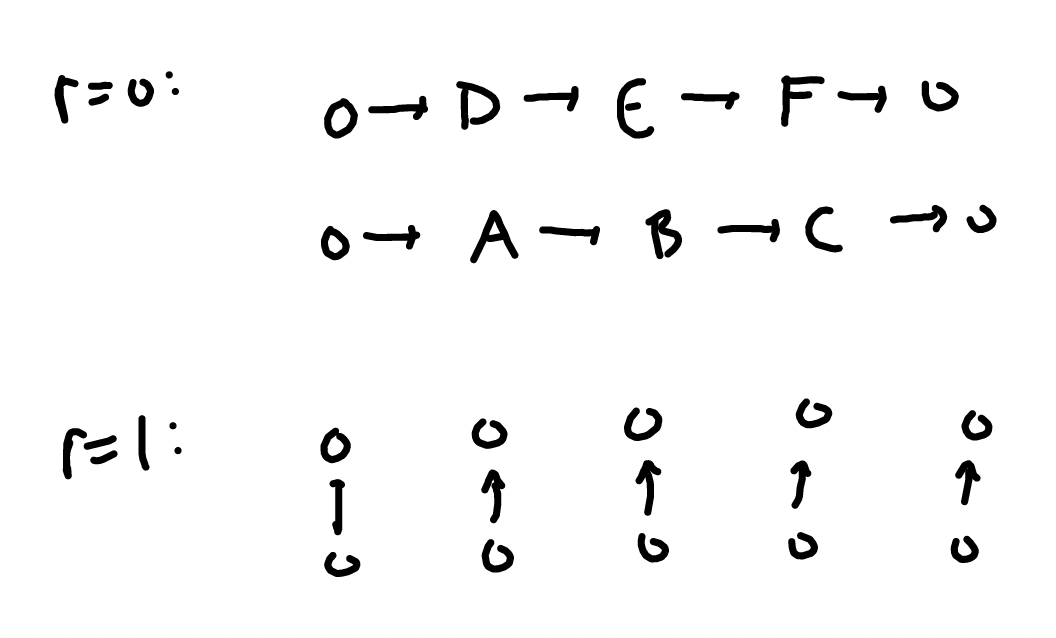
We can say that the spectral sequence collapsed at $r=1$, and we can deduce that $E_{\mathrm{\infty }}^{p,q}=0$ for every $p,q\ge 0$. Assuming the theorem which tells us this spectral sequence converges to $H^{\bullet }$, this forces $H^{\bullet }=0$.

On the other hand, using the vertical arrows in the original double complex produces a spectral sequence with upward orientation. The first three pages of the spectral sequence now look as follows:

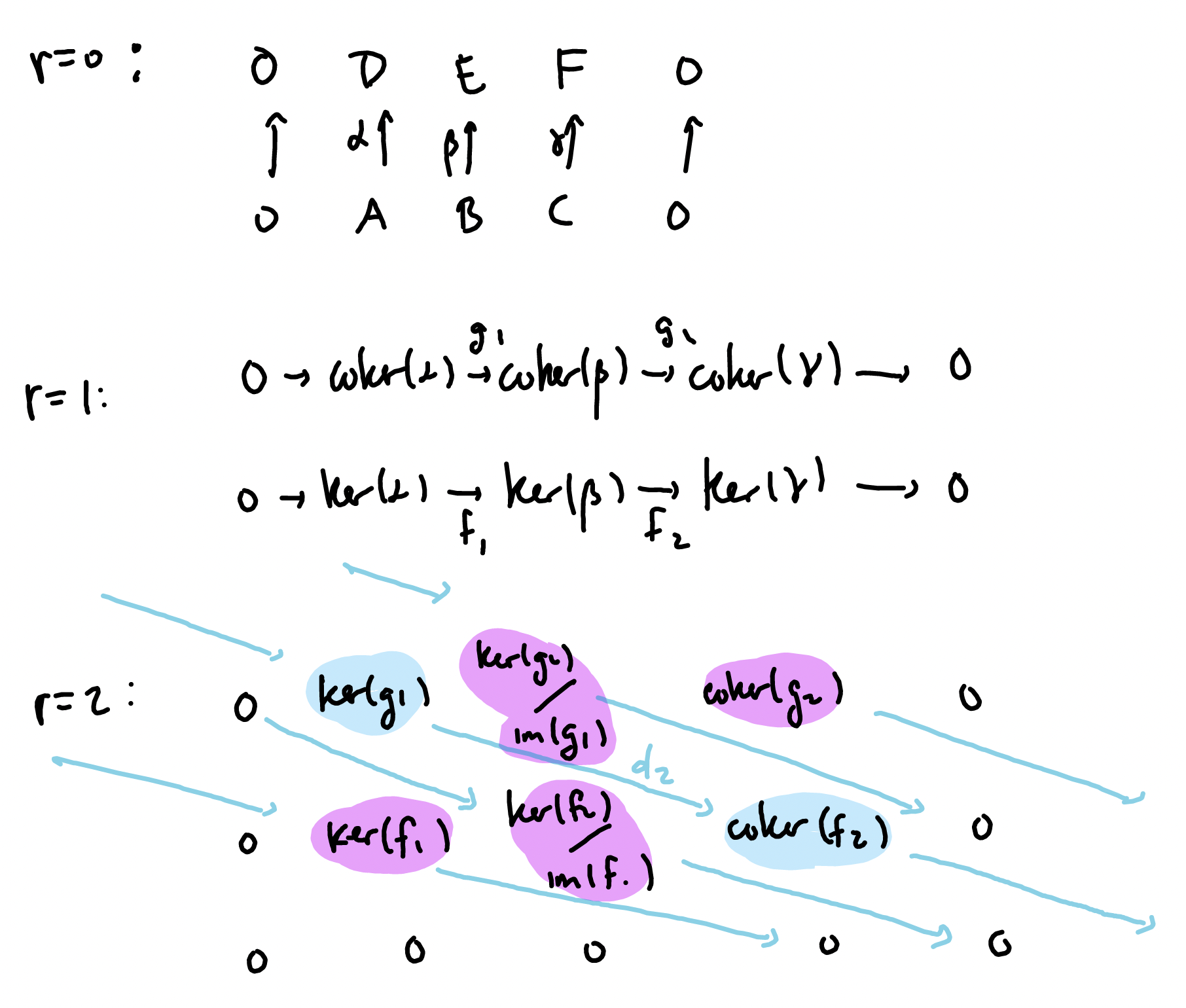
The terms highlighted in pink have stabilized at this point, as they do not (nor ever will) have nontrivial differentials mapping to/from them. The terms in blue will stabilize on the next page.

Now, this spectral sequence also converges to $H^{\bullet }$, which we earlier concluded was completely trivial. This implies that our second spectral sequence must also have $E_{\mathrm{\infty }}^{p,q}=0$ for all $p,q\ge 0$. In particular, the entries marked in pink above must all vanish, and the entries marked in blue must be isomorphic (via $d_2$). Together, these imply that we an exact sequence

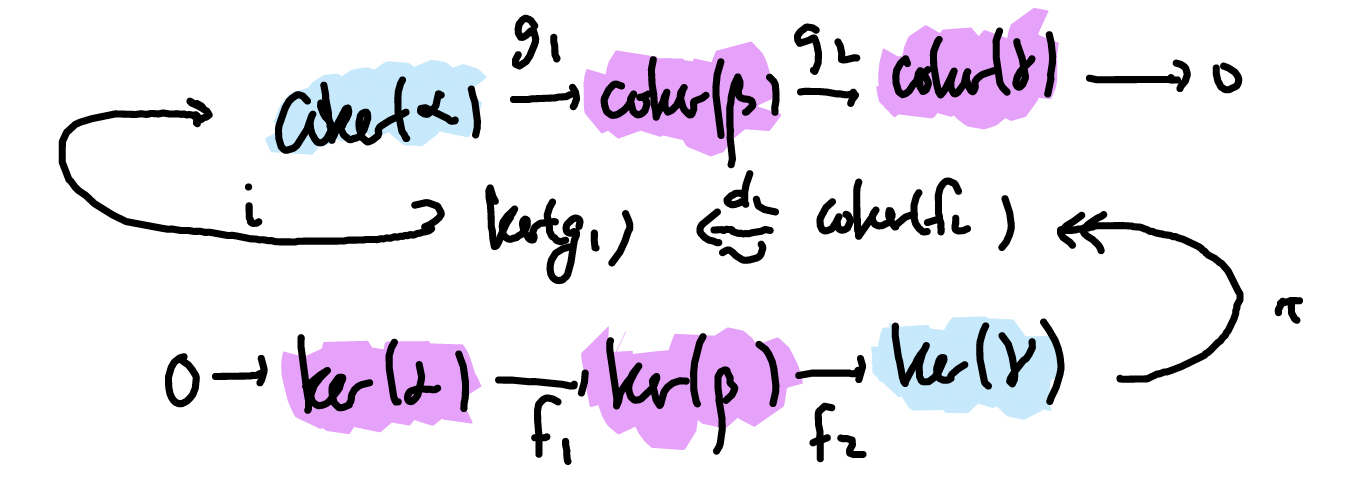
where the connecting morphism is $i\circ d_2\circ \pi$ (where $i$ is the appropriate inclusion of a kernel and $\pi$ is the appropriate projection onto a cokernel). This is exactly the conclusion of the Snake Lemma.

Example: The (Weak) Five Lemma

Suppose we begin with the commutative diagram below, where the rows are exact and the outside four vertical arrows are isomorphism. (This second condition can be weakened.)

Let's repeat the same strategy from the previous example. Beginning with the rightward orientation leads to a spectral sequence with the following first three pages:

Notice that this spectral sequence has collapsed at $r=2$, and that we can now conclude $H^2=0$ and $H^3=0$, where $H^{\bullet }$ is the cohomology of the double complex.

If we now instead consider the upward orientation, we find a spectral sequence that converges at $r=2$:

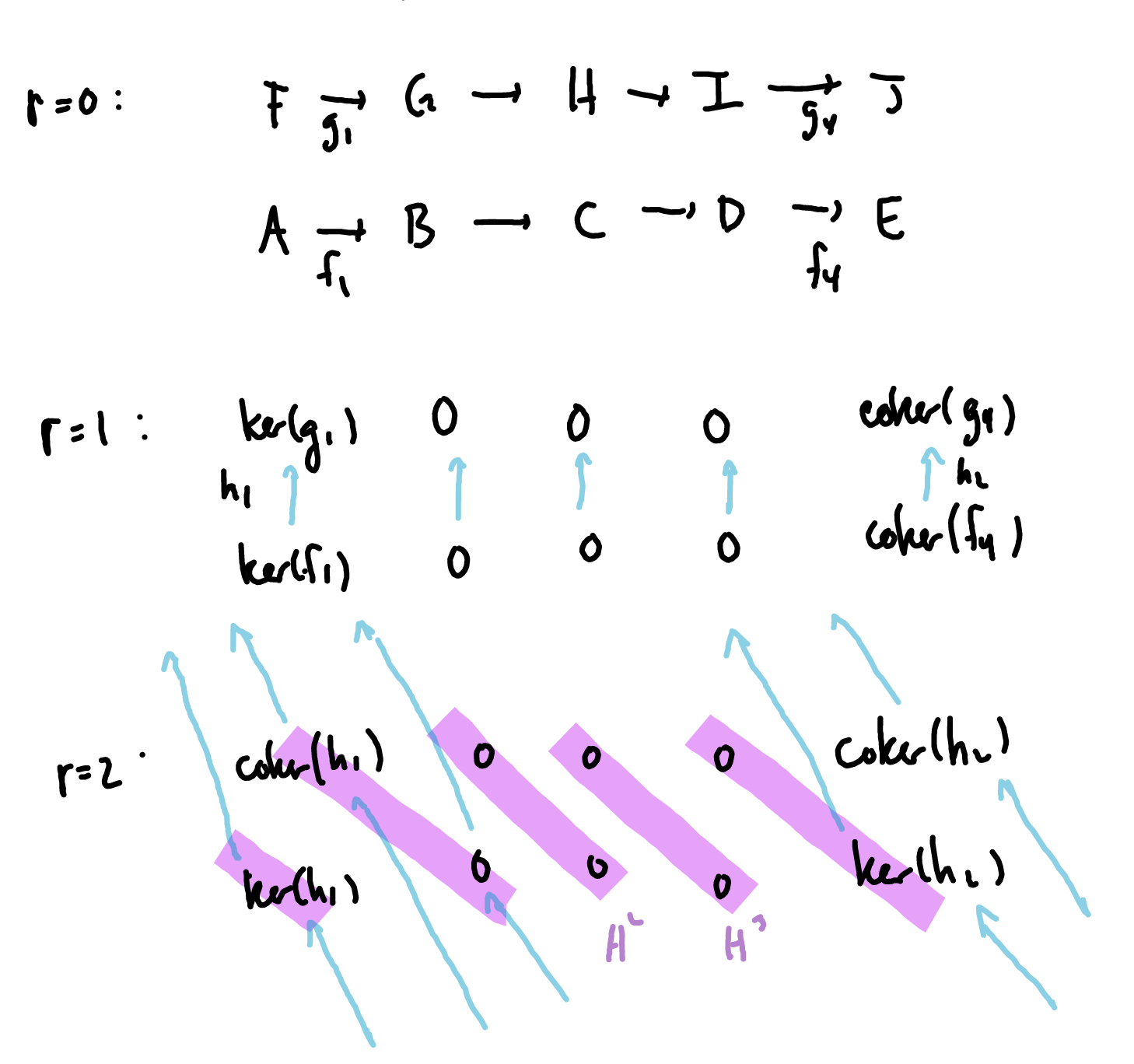
Since we earlier concluded $H^2=0$, the above spectral sequence tells us we must have $\ker (\gamma )=0$; since we also concluded $H^3=0$, the above spectral sequence also tells us we must have $\mathrm{coker}(\gamma )=0$. Together these imply $\gamma$ must be an isomorphism.

Example: The Grothendieck spectral sequence

This isn't really an example so much as hint at another scenario in which spectral sequences appear.

Suppose $F:\mathcal{A}\to \mathcal{B}$ and $G:\mathcal{B}\to \mathcal{C}$ are two additive and left exact functors between abelian categories. (For technical reasons, also assume both $\mathcal{A}$ and $\mathcal{B}$ have enough injectives, and that $F$ take injective objects in $\mathcal{A}$ to $G$-acyclic objects in $\mathcal{B}$.)

It makes sense to ask how the right derived functor of the composition $G\circ F$ relates to the composition of the right derived functors $RG$ and $RF$. Here's the theorem:

References

[[Chow - You Could have Invented Spectral Sequences.pdf]]
[[McCleary - A History of Spectral Sequences.pdf]]
[[Bott-Tu - Differential Forms in Algebraic Topology.pdf]]
[[Kato - Heart of Cohomology.pdf]]
[[McCleary - A Users Guide to Spectral Sequences.pdf]]
[[Vakil - Puzzlin Through Exact Sequences.pdf]]
[[Vakil - The Rising Sea.pdf]]

Suggested next note